Векторная алгебра для чайников. Урок 1. Понятие вектора.
Чтобы понять, что такое векторная алгебра, нужно сначала понять, что такое вектор, ибо векторная алгебра занимается изучением векторов. Существует несколько понятий вектора. Одно из них - это геометрическое понятие. Согласно этому понятию, вектор — это направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом. Если говорить простыми словами, то вектор - это стрелка*:
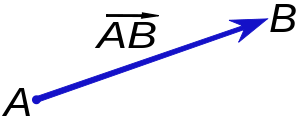
На рисунке мы видим вектор, начинающийся в точке
A и заканчивающиеся в точке B.
Такой вектор обозначается
![]() .
Вектора также могут обозначаться малыми латинскими буквами со стрелкой
наверху, например так
.
Вектора также могут обозначаться малыми латинскими буквами со стрелкой
наверху, например так
![]() или
просто с черточкой:
или
просто с черточкой:
![]() .
.
Для чего нужны векторы? Для указания направленной величины. Например, скорость. Направление стрелки указывает, куда движется объект, а длина стрелки - с какой скоростью. См. также урок Физика для чайников. Урок 3. Кинематика. Величина, которая имеет направления и поэтому задается вектором называется векторная величина. Как я уже сказал, такой величиной является скорость, сила (из физики). См. также Физика для чайников. Урок 7. Статика.
Кроме векторных величин, существует также скалярные величины - они не имеют направления. К таким величинам относится, например, температура, энергия, и другие.
Как правило, начало и конец векторов можно переносить параллельно друг другу на одинаковое расстояние. Это называется параллельный перенос. Такой параллельный перенос, как правило, используется при сложении векторов: начло одного вектора совмещается с концом другого и в результате получается сумма векторов. Но до операций над векторами мы еще дойдем. А пока идем дальше.
Итак, виды векторов:
-
Свободные вектора. Для них может быть применена операция параллельного переноса без ограничений. Равенство таких векторов означает, что равны их длины и направления. Существует также и строго определение равенства свободных векторов: свободные вектора
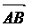 и
и
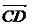 равны, если найдутся точки E и
F такие, что четырехугольники ABFE
и CDFE - параллелограммы.
равны, если найдутся точки E и
F такие, что четырехугольники ABFE
и CDFE - параллелограммы. -
Скользящие вектора. Такие вектора можно перемещать только вдоль прямой, на которой лежит данный вектор. Равенство скользящих векторов означает, что они лежат на одной прямой и равны их длины. Строгое определения равенства: скользящие вектора
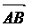 и
и
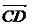 равны,
если точки A, B, C, D располагаются на одной прямой, а
сами вектора
равны,
если точки A, B, C, D располагаются на одной прямой, а
сами вектора
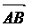 и
и
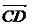 равны как свободные вектора.
равны как свободные вектора. -
Фиксированные вектора. Эти вектора перемещать нельзя вообще. Они как бы жестко закреплены. Равными фиксированные вектора считаются только в том случае, если они вообще совпадают - совпадают их начала и концы. Строгое определение: фиксированные вектора
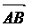 и
и
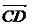 равны,
если попарно совпадают точки A и C,
B и D.
равны,
если попарно совпадают точки A и C,
B и D.
Для чего введена такая классификация векторов? Дело в том, что в некоторых случаях эти ограничения действительно имеют место быть. Например, в механике (см. также урок Физика для чайников. Урок 2. Механика). Возьмем, например, рычаг. Есть ли разница, какой точке приложена сила? Безусловно, есть. Вы знаете, что чем длиннее рычаг, тем легче его поворачивать: усилия одинаковые (то есть, равны свободные вектора этих сил), но точки приложения сил разные и разный производимый ими эффект.
Кроме геометрического, вектор также имеет и координатное представление. В общем случае (в пространстве) вектор раскладывается по трем координатам. Вектор на плоскости - это частный случай вектора и он раскладывается две координатные оси.
Разложение вектора по координатам выглядит вот так:
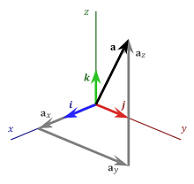
На данном рисунке мы видим вектор
![]() ,
который разложен на три вектора, получаемых умножением векторов
,
который разложен на три вектора, получаемых умножением векторов
![]() ,
,
![]() ,
,
![]() на координаты:
на координаты:
![]()
Вектора
![]() ,
,
![]() ,
,
![]() являются
единичными векторами и называются орты.
являются
единичными векторами и называются орты.
Если известны координаты начала и конца вектора, то координаты самого вектор а получаются путем вычитания координат конца вектора из координат его начала:
![]()
Как я уже говорил, вектор в общем случае задается в пространстве тремя координатами, то есть, для его определения используют три числа. В частном случае, вектор на плоскости может быть задан в виде двух чисел. Еще бывает вектор в n-мерном пространстве. Вообразить такой вектор сложно, но, тем не менее, это реальная математическая абстракция, которая представляет собой просто набор чисел. Чем то такой вектор напоминает множество, с той лишь разницей, что во множестве могут быть любые элементы и не важно в каком порядке они стоят, а вот в случае с вектором он задается только числами и как эти числа заданы, в таком же порядке они должны стоять. Например, если вектор задан числами {5,7,2,7,11,3} то именно в таком порядке и должны стоять числа.
Длина вектора называется его модулем и обозначается так:
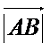 ну
или вот так:
ну
или вот так:
![]()
* «Vector AB from A to B» участника Изначально этот файл был загружен участником Silly rabbit из английский Википедия - Перенесено с en.wikipedia на Викисклад.. Под лицензией CC BY-SA 3.0 с сайта Викисклада - https://commons.wikimedia.org/wiki/File:Vector_AB_from_A_to_B.svg#/media/File:Vector_AB_from_A_to_B.svg