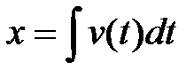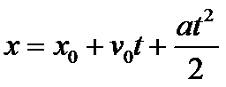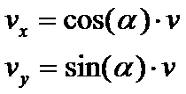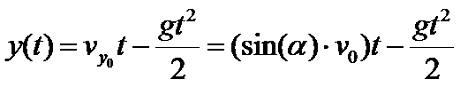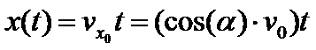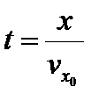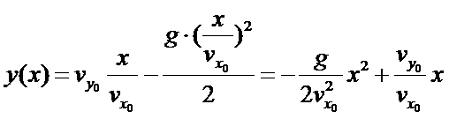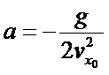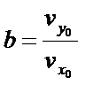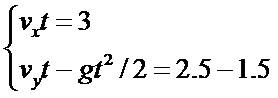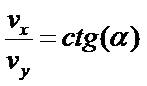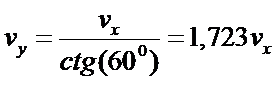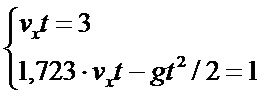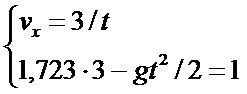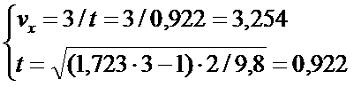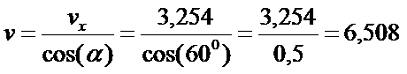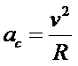Физика для чайников. Урок 3. Кинематика.
См. также видеоуроки:
Как и обещал, сейчас мы будем изучать кинематику. О ней я вкратце писал на прошлом уроке. Напомню, движение любого физического тела (объекта, предмета) может быть само по себе, без всякого воздействия на него какой либо силы (см. прошлый урок). Сила нужна только для того, что бы изменить скорость или направления движения. Так же движение происходит всегда относительно какой либо системы отчета. Что такое система отчета? Это некий наблюдатель, вокруг которого находиться пространство, и в этом пространстве наблюдатель видит движение различных тел. В зависимости от того, где находиться наблюдатель, будет разный характер движения. Например, на перроне стоит человек и видит движущийся поезд. Он наблюдает, что поезд движется относительного него. А вот человек в поезде видит другую картину - движется наблюдатель на перроне, который самому себе кажется неподвижный. Но на самом деле и тот и другой еще и вращается вместе с Землей вокруг Солнца. Так что если бы в центре Солнца мог сидеть какой то гипотетический наблюдатель, он бы увидел, что два этих объекта (человек на перроне и поезд) вращаются вокруг него, но поезд еще и постепенно перемещается в сторону от человека. Но мало того, само Солнце вращается вокруг центра Галактики, а вместе с ним тот гипотетический наблюдатель, сама Земля, а так же поезд на ней и человек на перроне. И сама наша Галактика тоже перемещается по Вселенной.
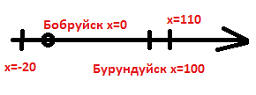
Уф, как все сложно! - скажете вы. Но не пугайтесь, тут мы будем рассматривать очень простые движения относительно очень простых систем отчета. Достаточно понять эти самые очень простые закономерности движения, что бы потом понимать и более сложные движения. И так, начнем с прямолинейного равномерного движения. Давайте представим, что из некоторого гипотетического города Бобруйск в некий гипотетический город Бурундуйск едет автомобиль. Допустим, между этими городами абсолютно прямая дорога. Расстояние между ними 100 км. Но давайте напряжем свое воображение и представим эту дорогу, уходящую в бесконечность. С другой стороны Бобруйска уходит в бесконечность такая же дорога. Получается, что мы имеем бесконечную прямую линию, на которой лежат две точки: город Бобруйск и город Бурундуйск. Третья точка - это автомобиль, который где то находиться на этой прямой. Он может иметь какое то расстояние от любого из этих городов. Если автомобиль все еще в центре Бобруйска, то его расстояние от него будет равно нулю. Таким образом, мы можем для определения местоположения автомобиля определять его расстояние от центра Бобруйска. В этом случае получается, что Бобруйск - это начала координат. Если автомобиль поехал в Бурундуйск, то его координата будет положительным числом, а если в другую сторону - то отрицательным. Обозначим это число x. Тогда, если автомобиль в Бобруйске, то x=0 км. Если в Бурундуйске, то x=100 км. Если машина проехала Бурундуйск на 10 км, то x=110 км. Если автомобиль поехал от Бурундуйска в обратную сторону и проехал 20 км, то его координата x равна -20 км:
Нетрудно догадаться, что если автомобиль будет ехать со скоростью 50 км/час, то от Бобруйска до Бурундуйска он доедет за 2 часа. А, например, через 5 часов он доберется до точки с координатой x=250. Разумеется, это при условии, что его скорость будет постоянной (без остановок, замедлений и ускорений). Разумеется, в жизни так не бывает. Но в любом случае, иногда происходят ситуации, когда какой то объект действительно движется с постоянной скоростью. Ну, или почти с постоянной - когда изменение скорости настолько маленькое, что мы этого не замечаем и такими колебаниями можно пренебречь. В таком случае движение называется равномерным. Если при этом движение идет по прямой, то это будет равномерное прямолинейное движение. Его можно описать вот такой простой формулой:
|
x=x0+vt |
(3.1) |
где x - координата объекта, v - его скорость за единицу времени, t - время, прошедшее с момента начала отчета, x0 - начальная координата объекта.
Таким образом, если, допустим, автомобиль в момент начала отчета времени находиться в Бурундуйске, и ехал по направлению к Бобруйску со скоростью 30 км/час, то через 2 часа его координата будет:
x=100-30*2=40.
Почему мы берем скорость со знаком "минус"? Потому что едем в обратную сторону, в сторону уменьшения координаты x.
А если нам нужно найти не местоположение, а например, время или начальную точку? Без проблем, выводим из этой формулы уравнение и решаем его. Через сколько будет автомобиль в Бурундуйске, если он уже отъехал от Бобруйска на 50 км и едет со скоростью 25 км/час? Составляем уравнение:
100=50+25t
Решаем:
t=(100-50)/25=2.
Таким образом, автомобиль доберется до места назначения через два часа.
Теперь поговорим об относительности движения. Давайте представим, что из Бобруйска вышел автомобиль со скоростью 50 км/ч, а из Бурундуйска ему навстречу вышел автомобиль со скоростью 70 км/ч. В этом случае с точки зрения водителя машины, которая выехала из Бобруйска, встречный автомобиль будет приближаться к ней со скоростью 120 км/час. Иными словами, поменяв систему отчета (заметьте, новая система отчета сама движения относительно предыдущей системы отчета), мы увидели совсем иной характер движения.
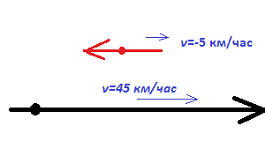
Представим, что из Бобруйска в Бурундуйск вышел поезд. И рельсы, по которым он идет, находятся рядом с автодорогой дорогой и такие же прямые. Поезде идет со скоростью 45 км/ч. Один из пассажиров вышел из своего купе и пошел в туалет со скоростью 5/км час. Туалет находиться впереди по ходу поезда. Какова будет скорость данного пассажира относительно Бобруйска? Правильно, 50 км/ч - в данном случае скорости складываются. А если он пошел обратно, то его скорость будет со знаком минус, в таком случае относительно Бобруйска он уже будет перемещаться со скоростью 40 км/час.
Вообще, что бы перевести скорость из одной системы отчета в другую, относительно которой движется первая система отчета, то скорости складываются, если координатная ось направлена в одну и ту же сторону. Если в первой системе отчета направление противоположной тому, которое принято в той систему, куда мы переводим, то скорость в перовой системе отчета надо прибавить с другим знаком. Иными словами, если бы в том поезде было принято, правило, что вперед - означает в сторону Бобруйска, то в случае, когда пассажир идет по ходу поезда, его скорость была бы отрицательна, а когда идет обратно - то положительна. Иными словами, двигаясь к туалету, пассажир шел бы со скоростью -5 км/час относительно системы отчета "поезд". Но так как оси координат этой системы направлены в противоположную сторону, то мы вычитаем, а не прибавляем эту скорость. Минус на минус дает плюс, в итоге получается, что мы все равно прибавляли 5 км/час:
И так, мы разобрали идеальный случай движения - равномерное прямолинейное. Но так не бывает. Точнее, бывает, но очень редко. А если еще точнее, то такое может случиться только в том случае, если изменением скорости можно пренебречь. Например, когда водитель автомобиля точно жмет на педаль акселератора и выдерживает постоянную скорость. Но в основном он то ускоряется, то замедляется. Поэтому мы рассмотрим еще один вид прямолинейного движения - равноускоренное (или равнозамедленное - тоже, но со знаком минус). При таком движении скорость выражается формулой:
|
v=v0+at |
(3.2) |
где v - скорость в момент времени t, v0 - значение скорости в начальный момент времени (с начала отчета времени), a - ускорение. Если идет замедление, то ускорение берется со знаком минус. Но как в таком случает определить пройденное расстояние? Формулу для него мы можем вывести, проинтегрировав функцию зависимости скорости от времени (формула 3.2):
|
(3.3) |
Решив данный интеграл, получим (увы, если вы не знакомы с математическим анализом, то вам просто придется этот вывод принять на веру, либо изучить этот самый матанализ, но это уже выходит за рамки данных уроков, хотя вы можете заглянуть в математическое приложение 1):
|
(3.4) |
Таким образом, теперь мы можем решить задачу для случая, когда в движении присутствует ускорение или замедление. Например, автомобиль тронулся в начальный момент времени из точки, обозначающую начала координат, при этом его ускорение было 2 м/с2, после чего он ехал с постоянной скоростью 72 км/час в течении 2 минут, после чего затормозил в течении 4 секунд. Вопрос, сколько метров прошел автомобиль?
В этом случае задачу можно разбить на три части. Сначала он двигался равноускоренно, мы не знаем в течении какого времени, но знаем какой скорости достиг 72 км/час - это 20 м/с. При ускорении 2 м/с2 он достигнет этой скорости за 10 секунд и пройдет расстояние 2*102/2=100 м. Дальше он двигался равномерно в течении 120 секунд, за это время машина проехала 20*120=2400 метров. Если автомобиль тормозил 4 секунды, то его ускорение было 20/4=5 м/с2, а тормозной путь, соответственно, 5*42/2=40 м. В итоге машина прошла 2540 метров.
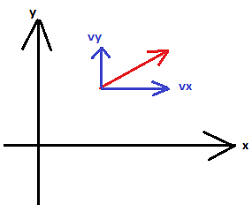
Ну а теперь мы знаем достаточно, что бы перейти к криволинейному движению. Это тоже самое, что прямолинейное, но вместо координаты x добавляется еще y, или y и z - для случая, когда мы рассматриваем движение в пространстве. Как видим, ничего сложного, только чуть больше вычислений. В каком бы направлении не двигалось физическое тело, его скорость, ускорение и пройденный путь можно разложить по координатам. Для того, что бы понять, как это делается, нам надо познакомиться с понятием вектор. Вектор - это такая стрелочка, которая указывает направление. И любой вектор как раз и раскладывается на векторы по координатам. Рассмотрим, как он раскладывается на плоскости:
Как его разложить? Надо знать угол между данным вектором и ось координат x. Тогда мы сможем воспользоваться тригонометрическими функциями:
|
(3.5) |
где α - угол наклона к горизонту.
Рассмотрим два наиболее важных криволинейных движения: парабола и окружность.
По параболической траектории, как известно, движется физическое тело, брошенное под углом к горизонту. Разумеется, в том случае, когда сопротивлением воздуха можно пренебречь. Например, массивное такое, тяжелое, пушечное ядро.
А теперь я приведу доказательства данного утверждения. И так, согласно закону всемирного тяготения, любое физическое тело падает на Землю с постоянным ускорением, не зависимым от массы тела. Возле поверхности земли это ускорения равно g. Это приблизительно 9/8 м/с2. Таким образом, высоту, на которое будет находиться физическое тело в момент времени t, брошенное к горизонту, можно выразить формулой:
|
(3.6.) |
где y(t) - зависимость высоты (координаты y) от времени t, α - угол наклона к горизонту, v0 - начальная скорость, t - момент времени. Высота вычисляется относительно начального положения брошенного тела.
Местоположение брошенного под углом тела по горизонтали в момент времени t мы можем вычислить по формуле
|
(3.7) |
Выразим t через x:
|
(3.8) |
Подставим x в формулу 3.6:
|
(3.9) |
Что у нас получилось? По сути, квадратное квадратичная функция вида:
|
y(x)=ax2+bx+c=0 |
(3.10) |
где
|
(3.11) |
|
(3.12) |
c в данном частном случае равно 0. В общем случае оно зависит от начальной высоты, с которой объект был брошен.
График квадратичной функции - парабола. Так как зависимость координаты y от координаты x имеет вид квадратичной функции, то, значит, траектория объектов у нас тоже будет парабола.
А теперь попробуем решить задачу. Пусть баскетболист бросает мяч в корзину. В момент броска мяч находился на высоте 1,5 метра. Высота корзины над уровнем пола - 2.5 метра. Расстояние по горизонтали до корзины - 3 метра. Какая начальная скорость мяча, если мяч попал точно в корзину и был брошен под углом к горизонту 600?
Сначала разложим начальную скорость мяча на горизонтальную и вертикальную, Вычислив коэффициенты от начальной скорости.
sin(600)=0,866
cos(600)=0,5
Из формул зависимости высоты и горизонтального перемещения получим вот такую систему уравнений:
|
(3.13) |
Очевидно, что для решения данной системы нам потребуется выразить vy через vx, получим его из следующего соотношения:
|
(3.14) |
где α - угол, под которым тело брошено к горизонту. Отсюда:
|
(3.15) |
Таким образом, мы можем представить это уравнение в виде:
|
(3.16) |
Выразим vx через t:
|
(3.17) |
Теперь мы без труда сможем решить эту систему уравнений:
|
(3.18) |
Теперь мы знаем скорость по горизонтали vx=3,254 м/с. Из формулы 3.5 выразим v:
|
(3.19) |
Таким образом, скорость мяча в начальный момент времени приблизительно 6,5 м/с.
Проверим, правильно ли мы решили задачу. И так, вычислим вертикальную скорость vy=sin(600)*6,508=5,636 м/с. Спустя время t мяч окажется на высоте vyt-gt2/2 относительно точки броска, то есть: 5,636*0,922-9,8*0,9222/2=5,196-4,165=1,011≈1 м. В нашем случае, так и есть: корзина на высоте 2,5 м, мяч брошен с высоты 1,5 м, разница 1 метр. Так же нетрудно посчитать, что мяч пролетит за время броска 3 метра в горизонтальном направлении 3,254*0,922=3,000188≈3 м.
Обратите внимание, что все вычисления мы делаем с определенной погрешностью, если хотите посчитать более точно, то не округляйте промежуточные расчеты или округляйте до больших знаков после запятой, чем округлили мы в нашей задаче.
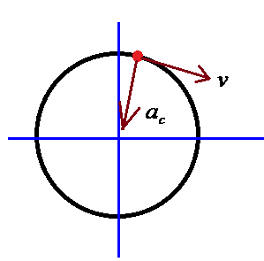
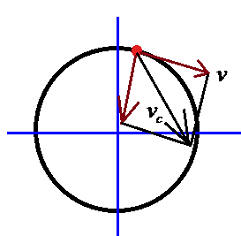
Теперь рассмотрим еще один вид криволинейного движения: движение по окружности. Оно так же в каждый момент времени раскладывается на два вектора. Но что характерно, в отличии от движения тела, брошенного под углом к горизонту, один из векторов всегда направлен к центру окружности, а второй перпендикулярен ему. Тот, что направлен к центру окружности - это вектор центростремительного ускорения, а перпендикулярный ему - это вектор постоянно скорости:
Почему именно так? Давайте разберемся. Представим, что вектора ac нет. Тогда тело будет двигаться по прямой вдоль вектора v. А если вместо ac будет просто вектор скорости (равномерное движение)? Тогда они просто сложатся:
То есть, тело опять же будет двигаться по прямой. Что же надо сделать, что бы тело двигалось по окружности? А надо для этого, что бы оно в каждый момент времени меняло направление, стремясь к центру окружности. Вот отсюда и центростремительное ускорение. Естественно, оно должно быть равно строго определенной величине. Если будет меньше - тело начнет по спирали удаляться от центра окружности, если больше - по спирали приближаться. Но не вечно, а лишь до того момента, пока радиус не достигнет той величины, когда центростремительное ускорение будет равно тому, при котором тело станет двигаться по окружности. Связь между радиусом окружности, линейной скоростью по касательной и центростремительным ускорением можно выразить формулой:
|
(3.20) |
где v - линейная скорость по касательной, ac - центростремительное ускорение, R - радиус окружности.
См. также видеоуроки: