Математический анализ для чайников. Урок 1. Множества.
Понятие множества
Множество - это совокупность некоторых объектов. Какие могут быть множества? Во первых, конечные или бесконечные. Например, множество спичек в коробке - это конечное множество, их можно взять и сосчитать. Количество песчинок на пляже сосчитать гораздо труднее, но, в принципе, возможно. И это количество выражается каким то конечным числом. Так что множество песчинок на пляже тоже конечно. А вот множество точек на прямо это множество бесконечное. Так как во первых, прямая сама по себе бесконечная и на ней можно поставить сколько угодно точек. Множество точек отрезка прямой тоже бесконечное. Потому что теоретически точка может быть сколь угодно маленькая. Конечно, мы физически не сможем нарисовать точку, размером, например, меньше размера атома, но, с точки зрения математики точка не имеет размера. Ее размер равен нулю. А что получается, если разделить на нуль какое то число? Правильно, бесконечность. И хотя множество точек на прямой и на отрезке стремится к бесконечности, это не одно и тоже. Множество - это не количество чего то там, а совокупность каких либо объектов. И равными считаются только те множества, которые содержат абсолютно одинаковые объекты. Если в одном множество содержит те же объекты, что и другое множество, но плюс еще один какой нибудь "левый" объект, то это уже не равные множества.
Рассмотрим пример. Пусть у нас имеется два множества. Первое - совокупность все точек на прямой. Второе - совокупность всех точек на отрезке прямой. Почему они не равны? Во первых, отрезок и прямая могут даже не пересекаться. Тогда они уж точно не равны, так как содержат в себе абсолютно разные точки. Если они пересекаются, то у них только одна общая точка. Все остальные так же разные. А если отрезок лежит на прямой? Тогда все точки отрезка являются и точками прямой. Но не все точки прямой являются точками отрезка. Так что и в этом случае множества нельзя считать равными (одинаковыми).
Каждое множество задается правилом, которое однозначно определяет, принадлежит элемент к этому множеству или нет. Какие могут быть эти правила? Например, если множество конечное, можно тупо перечислить все его объекты. Можно задать диапазон. Например, все целые числа от 1 до 10. Это будет тоже конечное множество, но тут мы не перечисляем его элементы, а формулируем правило. Или неравенство, к примеру, все числа, больше 10. Это будет уже бесконечное множество, поскольку нельзя назвать самое большое число - какие бы число мы не называли, всегда есть это число плюс 1.
Как правило, множества обозначаются прописными буквами латинского алфавита A, B, C и так далее. Если множество состоит из конкретных элементов и мы хотим задать его списком этих элементов, то мы можем заключить этот список в фигурные скобки, например A={a, b, c, d}. Если a является элемент множества A, то это записывают следующим образом: a Î A. Если же a не является элементом множества A, то пишут a Ï A. Одним из важных множеств является множество N всех натуральных чисел N={1,2,3,...,} . Существует также специальное, так называемое пустое множество, которое не содержит ни одного элемента. Пустое множество обозначается символом Æ .
Определение 1 (определение равенства множеств). Множества А и B равны, если они состоят из одних и тех же элементов, то есть, если из x Î A следует x Î B и обратно, из x Î B следует x Î A.
Формально равенство двух множеств записывается следующим образом:
(А=В):= " x((x Î A) Û (x Î B)),
это означает, что для любого объекта x соотношения xÎ A и xÎ B равносильны.
Здесь " – квантор всеобщности (" x читается как "для каждого x").
Определение 2 (определение подмножества). Множество А является подмножеством множества В, если любое х принадлежащее множеству А, принадлежит множеству В. Формальное это можно представить в виде выражения:
(A Ì B) := " x ((x Î A) Þ (x Î B))
Если A Ì B, но A ¹ B, то A – собственное подмножество множества В. В качестве примера можно привести опять же прямую и отрезок. Если отрезок лежит на прямой, то множество его точек являются подмножеством точек этой прямой. Или, другой пример. Множество целых чисел, которые делятся без остатка на 3, является подмножеством множества целых чисел.
Замечание. Пустое множество является подмножеством любого множества.
Операции над множествами
Над множествами возможны следующие операции:
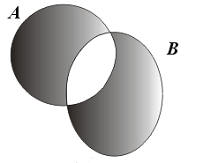
Объединение. Суть этой операции состоит в том, что бы два множества объединить в одно, содержащее элементы каждого из объединяемых множеств. Формально это выглядит так:
C=A È B: = {x:x Î A или x Î B}
Пример. Решим неравенство |2x+3| > 7.
Из него следует либо неравенство 2x+3 >7, для 2x+3≥0, тогда x>2
либо неравенство 2x+3 <-7, для 2x+3<0, тогда x<-5.
Множеством решений данного неравенство является объединения множеств (-∞,-5) È (2,∞).
Давайте проверим. Посчитаем значение выражение |2x+3| для нескольких точек, лежащих и не лежащих в данном диапазоне:
| x | |2x+3| |
| -10 | 17 |
| -6 | 9 |
| -5 | 7 |
| -4 | 5 |
| -2 | 1 |
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
| 5 | 13 |
Как видим, все решено правильно (красным обозначены пограничные диапазоны).
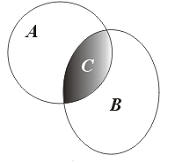
Пересечение. Пересечением называется операция создания нового множества из двух, содержащих элементы, которые входят в оба этих множества. Что бы изобразить это наглядно, давайте представим, что у нас есть два множества точек на плоскости, а именно фигура A и фигура B. Их пересечение обозначает фигуру C - это и есть результа операции пересечения множеств:
Формально операция пересечения множеств записывается так:
C=A Ç B := {x: x Î A и x Î B }
Пример. Пусть у нас есть множество A={1,2,3,4,5,6,7}, B={5,6,7,8,9,10}. Тогда C=A Ç B = {5,6,7}
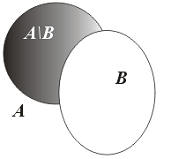
Вычитание. Вычитание множеств - это исключение из вычитаемого множества тех элементах, которые содержатся в вычитаемом и вычитателе:
Формально вычитание множества записывается так:
A \ B: = {x:x Î A и x Ï B}
Пример. Пусть у нас есть множество A={1,2,3,4,5,6,7}, B={5,6,7,8,9,10}. Тогда C=A \ B = {1,2,3,4}
Дополнение. Дополнение - это унарная операция (операция не над двумя, а над одним множеством). Эта операция является результатом вычитания данного множества из полного универсального множества (множества, которое включает в себя все остальные множества).
A: = {x:x Î U и x Ï A} = U \ A
Графически это можно изобразить в виде:
Симметричная разность. В отличии от обычной разности при симметричной разности множеств элементы остаются только те, что присутствуют либо в одном, либо в другом множестве. Или, говоря простым языком, из двух множеств создается, но из него исключаются те элементы, которые есть и в том и в другом множестве:
Математически это можно выразить так:
A D B:= (A \ B) È (B \ A) = (A È B) \ (A Ç B)
Свойства операций над множествами.
Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими свойствами:
- Коммутативность.
A
È
B=B È
A
A Ç
B=B Ç
A
- Ассоциативность.
(A
È
B)
È
C=A È
(B È
C)
(A Ç
B)
Ç
C= A Ç
(B Ç
C)
- Дистрибутивность.
(A
È
B)
Ç
C =
(A
Ç
C)
È
(B Ç
C)
(A Ç
B)
È
C=
(A
È
C)
Ç
(B È
C)
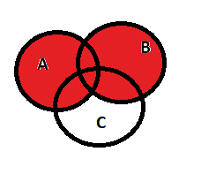
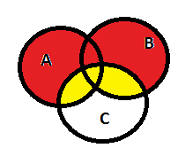
Проиллюстрируем первое свойство дистрибутивности картинкой (красным заштриховано A È B) :
Вычтем из него C ((A È B) Ç C, желтый цвет):
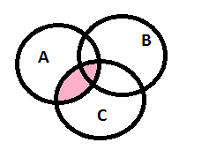
Теперь представим A Ç C (розовый цвет):
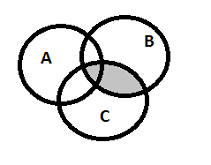
и B Ç C (серый цвет):
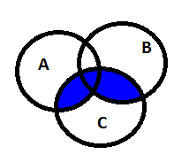
(A Ç C) È (B Ç C) - это серая закраска + розовая закраска. Обозначим ее синим цветом:
Следствия:
A
È
A=A, A Ç
A=A
A È Æ
= A, A Ç Æ=
Æ