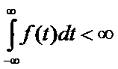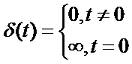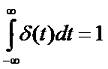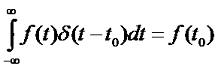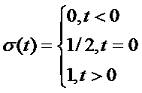| Цифровая обработка сигналов. Урок 5. Классификация сигналов |

|

|
| Автор megabax | |
| 12.12.2011 г. | |
Цифровая обработка сигналов. Урок 5. Классификация сигналовЭто последний урок из серии "Цифровая обработка сигналов", публикуемый в бесплатном разделе. Начиная со следующего, публикация уроков будет продолжена в платном разделе. В бесплатном же разделе иногда будут публиковать некоторые статьи, посвященные идеям и способам цифрового анализа сигналов. Основная цель анализа сигналов - сравнение их с друг другом для выявления сходств и различий. Можно выделить три основные составляющие анализа сигналов:
Рассмотрим сначала классификацию сигналов. Во первых, проверка принадлежности сигналов к конкретному классу уже является анализом сигналов. Во вторых, для анализа сигналов различных классов зачастую применяются разные подходы. И так, сигналы можно классифицировать по детерминированности. Различают детерминированные и случайны сигналы. К первым относятся те сигналы, которые полностью известны. Это те сигналы, значение которых в каждый момент времени можно определить точно. Случайные же сигналы принимают в каждый конкретный момент времени определенное значение лишь с какой то долей вероятности. Еще есть сигналы с интегрируемым квадратом. Еще их называют сигналом с ограниченной энергией. Для них справедливо условие: где f(t) - функция значения сигнала в каждый конкретный момент времени. Существуют так же периодические и непериодические сигналы. Для первых справедливо равенство: где n - любое целое число, T - период сигнала. Величина, обратная периоду F=1/T есть частота сигнала. Очевидно, что если периодический сигнал не равен нулю при любом t, то его энергия бесконечна. Если сигнал выражен формулой: где A - амплитуда, ω - угловая частота, φ - начальная фаза, то такой сигнал называется гармоническим сигналом. Существуют так же два типа теоретических сигналов. Первый из них - это дельта функция или функция Диарка. Этот сигнал выражается формулой: Данный сигнал может быть только в теории, на практике реализовать его невозможно. Но эта функция очень важна для теоретического анализа сигналов и систем. Площадь данной функции равна единице: Одно из важных свойств дельта функции так называемое фильтрующее свойство. Оно состоит в том, что если дельта функция стоит под интегралом в качестве множителя, то результат интегрирования будет равен значению остального подынтегрального выражения в той точке, где сосредоточен дельта импульс: Следующий теоретический сигал: функция единичного скачка. Она выражается формулой: Функцию единичного скачка удобно использовать для сигналов конечной длительности. Простейшим примером является формирование прямоугольного импульса с амплитудой A и длительностью T: Вообще, любую кусочно-заданную зависимость можно выразить в виде единого математического выражения, используя функцию единичного скачка.
|
|
| Последнее обновление ( 22.05.2013 г. ) |
| Пред. » |
|---|