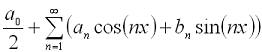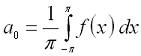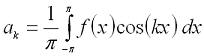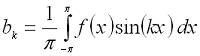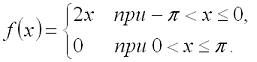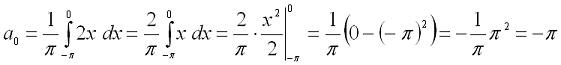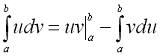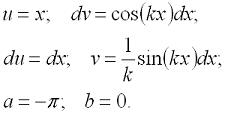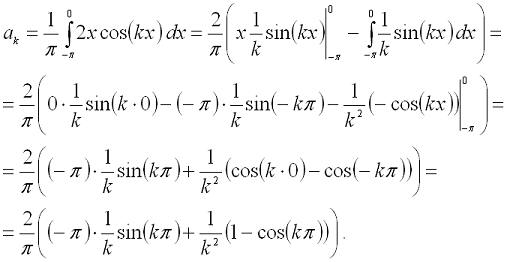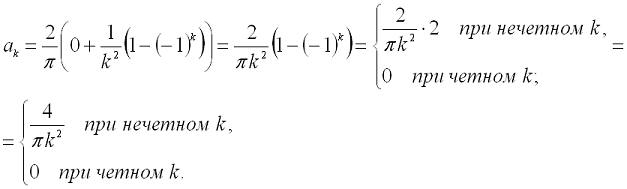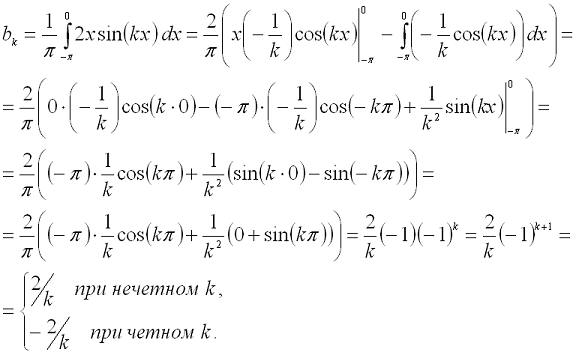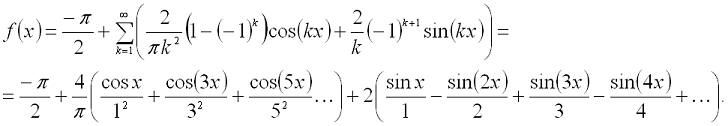| Цифровая обработка сигналов. Урок 1. Разложение в ряд Фурье. |

|

|
| Автор megabax | |
| 10.11.2011 г. | |
Цифровая обработка сигналов. Урок 1. Разложение в ряд Фурье.Любую периодическую функцию с периодом 2π, которая является кусочно-монотонной на отрезке [-π, π] можно разложить в ряд Фурье, то есть, представить ее виде бесконечной суммы гармонических функций (синусоид и косинусоид). Эту сумму можно представить формулой: где: Теперь рассмотрим пример. Разложим в ряд Фурье функцию, заданную формулой: И так, вычисляем a0: Теперь перейдем к ряду коэффициентов a. Тут мы применим интегрирование по частям, которое можно выразить формулой: где И так, вычисляем ak: Заметим, что sin(kπ)=0 при любом значении k, а cos(kπ)=1 при четном k и -1 при нечетном. Иными словами, мы можем преобразовать эту формулу к виду: Теперь переходим к bk: В результате получит вот такое разложение нашей функции в ряд Фурье: На этом мы закончим урок, а далее (на следующих уроках) будем проверять наши вычисления, используя программу Microsoft Excel и язык программирования C#.
|
|
| Последнее обновление ( 22.05.2013 г. ) |
| « След. |
|---|