|
unit AIObj
Создаем искусственный интеллект. Урок
5. Поиск решений задач в пространстве состояний. А-алгоритм.
Достоинство алгоритма равных цен состоит в том, что он гарантирует нахождение
оптимального пути. Достоинством алгоритмов, использующих оценку предстоящих
затрат ĥ(n),
является возможность усечения дерева поиска, что повышает эффективность поиска.
Естественным является стремление комбинировать эти алгоритмы и учитывать как
сделанные, так и предстоящие затраты. Этого можно добиться, если воспользоваться
оценочной функцией.
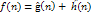 ,
,
где
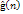 -
оценка стоимости пути из начальной вершины в вершину
n; -
оценка стоимости пути из начальной вершины в вершину
n;
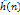 –
оценка стоимости кратчайшего пути из вершины
n
в целевую
вершину. –
оценка стоимости кратчайшего пути из вершины
n
в целевую
вершину.
Алгоритм, базирующийся на использовании оценочной функции
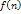 ,
называется А-алгоритмом. Оценки ,
называется А-алгоритмом. Оценки
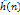 в ходе поиска не меняют своих значений.
Оценки в ходе поиска не меняют своих значений.
Оценки
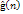 также не меняют своих значений и всегда равны реальным затратам
также не меняют своих значений и всегда равны реальным затратам
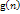 ,
если поиск пути выполняется на дереве
состояний. Однако при поиске пути на графе состояний оценки ,
если поиск пути выполняется на дереве
состояний. Однако при поиске пути на графе состояний оценки
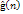 могут
меняться. Следовательно, в общем случае оценки могут
меняться. Следовательно, в общем случае оценки
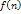 меняют
свои значения в процессе поиска. Это приводит к тому, что вершины из списка
CLOSED
могут перемещаться обратно в список
OPEN: меняют
свои значения в процессе поиска. Это приводит к тому, что вершины из списка
CLOSED
могут перемещаться обратно в список
OPEN:
Алгоритм,
базирующийся на использовании оценочной функции
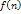 ,
называется А-алгоритмом. Оценки ,
называется А-алгоритмом. Оценки
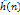 в
ходе поиска не меняют своих значений. Оценки в
ходе поиска не меняют своих значений. Оценки
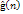 также
не меняют своих значений и всегда равны реальным затратам также
не меняют своих значений и всегда равны реальным затратам
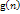 ,
если поиск пути выполняется на дереве
состояний. Однако при поиске пут ,
если поиск пути выполняется на дереве
состояний. Однако при поиске пут
-
Procedure A_Search;
-
Begin
-
Поместить начальную вершину
s в список
OPEN: f(s)=ĥ(s);
-
CLOSED := ’пустой
список’;
-
While OPEN <> ’пустой
список’
Do Begin
-
n := first(OPEN);
-
If n = ‘целевая
вершина’
Then Выход(УСПЕХ);
-
Переместить
n из списка OPEN в
CLOSED;
-
Раскрыть вершину
n,
для всех её дочерних вершин
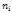 вычислить вычислить
-
оценку
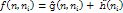 ; ;
-
Поместить дочерние
вершины, которых нет в списках
OPEN,
сравнить
-
оценки
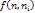 и и
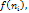 если если
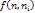 < <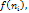 то
связать с вершиной то
связать с вершиной
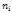 новую
оценку новую
оценку
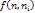 и
указатель на вершину n; и
указатель на вершину n;
-
Если вершина
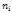 содержится
в списке CLOSED и содержится
в списке CLOSED и
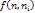 < <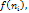
-
то связать с вершиной
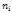 новую
оценку новую
оценку
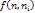 переместить
её в список OPEN и установить указатель на
n; переместить
её в список OPEN и установить указатель на
n;
-
Упорядочить список
OPEN
по возрастанию значения
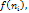 ; ;
-
End;
-
Выход(НЕУДАЧА);
-
End.
Укажем свойства А-алгоритма. Если для всех вершин
ĥ(n)=0,то
А-алгоритм будет соответствовать алгоритму равных цен. В этом случае
гарантируется нахождения оптимального пути, но эффективность поиска будет низкой,
и если пространство поиска будет бесконечно, то поиск просто не осуществим.
А-алгоритм не дает гарантии, что найденный путь будет оптимальным. Путь может быть не
оптимальным в случае, если оценка затрат на пути из вершины
n
в целевую
вершину будет преувеличена (переоценена), т.е. если ĥ(n)>h(n)
Сказанное можно пояснить с помощью рисунка:
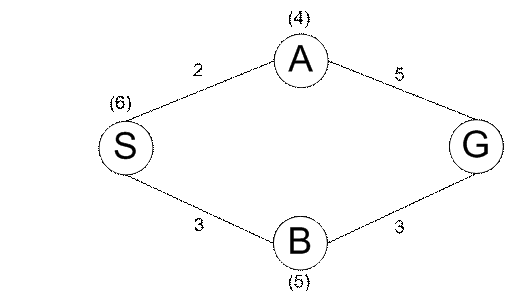
Рисунок
– граф состояний с переоценкой затрат h(n)
Числа
в скобках при вершинах соответствуют оценка ĥ(n),
а рядом с ребрами – стоимости перехода
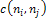 .
При раскрытии вершины
S
получаем дочерние вершины А и В. Оценки
f(n) для
этих вершин равны:
f(A)
= 2+4,
f(B)
= 3+5.
На следующем шаге раскрывается вершина А, и получается
f(G)
= 7+0.
Решением будет путь
S→A→G,
который для данного графа не является оптимальным. .
При раскрытии вершины
S
получаем дочерние вершины А и В. Оценки
f(n) для
этих вершин равны:
f(A)
= 2+4,
f(B)
= 3+5.
На следующем шаге раскрывается вершина А, и получается
f(G)
= 7+0.
Решением будет путь
S→A→G,
который для данного графа не является оптимальным.
А-алгоритм
обеспечит поиск оптимально пути, если выполняется условие: ĥ(n)≤h(n).
Алгоритм, учитывающий данное, называют А* - алгоритмом или гарантирующим
алгоритмом. А* - алгоритм недооценивает затраты на пути из промежуточной вершины
в целевую вершину или оценивает их правильно, но никогда не переоценивает.
Пусть
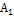 * и * и
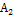 * - произвольные гарантирующие алгоритмы и на всех вершинах * - произвольные гарантирующие алгоритмы и на всех вершинах
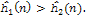 . Тогда информированность . Тогда информированность
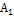 * выше, чем * выше, чем
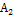 *. Говорят, что в этом случае *. Говорят, что в этом случае
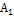 * имеет большую эвристическую силу, чем * имеет большую эвристическую силу, чем
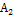 *. Эвристически более сильный алгоритм *. Эвристически более сильный алгоритм
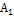 * в большей степени сокращает пространство поиска. * в большей степени сокращает пространство поиска.
Эффективность поиска с помощью А* - алгоритма может снижаться из-за того, что вершина, находящаяся в списке CLOSED, может попадать обратно с список OPEN и затем повторно закрываться. Следующий пример демонстрирует случай многократного раскрытия вершин.
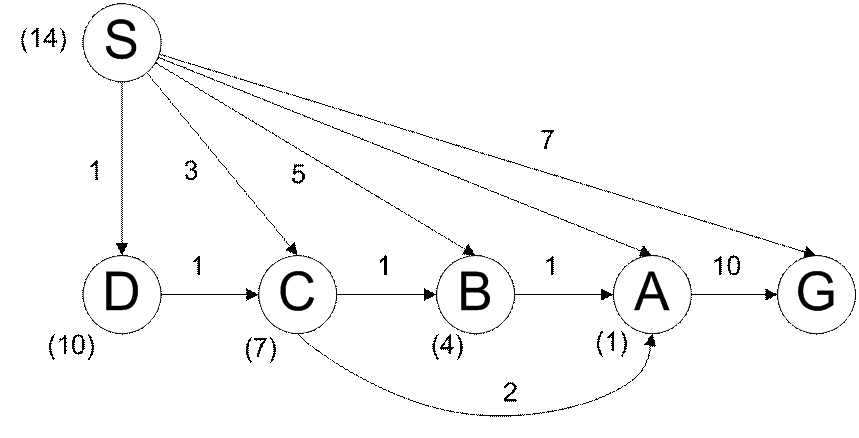
Рисунок - Граф состояний с многократно раскрываемыми вершинами.
Состояние списков OPEN и CLOSED показаны в таблице. Каждая строка таблицы соответствует очередному шагу работы алгоритма. Числа рядом с именами вершин соответствует значениям оценочной функции f(n). Из таблицы следует, что вершина А раскрывается четыре раза, вершина В – 3 раза, вершина С – 2 раза.
Таблица – Выполнение А*-алгоритма:
|
№ |
OPEN |
CLOSED |
Комментарий |
|
1 |
S(14) |
- |
|
|
2 |
A(8) B(10) C(10) D(11) |
S(14) |
|
|
3 |
B(9) C(10) D(11) G(17) |
A(8) S(14) |
|
|
4 |
A(7) C(10) D(11) G(17) |
B(9) S(14) |
Возврат: А |
|
5 |
C(10) D(11) G(16) |
A(7) B(9) S(14) |
|
|
6 |
A(6) B(8) D(11) G(16) |
C(10) S(14) |
Возврат: А, В |
|
7 |
B(8) D(11) G(15) |
A(6) C(10) S(14) |
|
|
8 |
D(11) G(15) |
B(8) A(6) C(10) S(14) |
|
|
9 |
C(9) G(15) |
D(11) B(8) A(6) S(14) |
Возврат: С |
|
10 |
A(5) B(7) G(15) |
C(9) D(11) S(14) |
Возврат: А, В |
|
11 |
B(7) G(14) |
A(5) C(9) D(11) S(14) |
|
|
12 |
G(14) |
B(7) A(5) C(9) D(11) S(14) |
|
Чтобы А*-алгоритм не раскрывал несколько раз одну и ту же вершину,
необходимо учитывать условие монотонности:
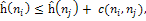
е
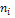 - родительская вершина; - родительская вершина;
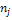 - дочерняя вершина, - дочерняя вершина,
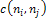 - стоимость пути между вершинами - стоимость пути между вершинами
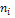 и и
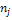 . .
Если условие монотонности соблюдается для всех дочерних вершин, то можно доказать, что в тот момент, когда раскрывается некоторая вершина n, оптимальный путь к ней уже найден. Следовательно, оценочная функция f(n) для данной вершины в дальнейшем не меняет своих значений, и никакие вершины из списка CLOSED в список OPEN не возвращаются.
Ранее отмечалось, что А* - алгоритм недооценивает затраты h(n). Условие монотонности означает, что недооценка на пути к цели становится все меньше или, в крайнем случае, не изменяется. Действительно, если обозначить недооценку через û(n), то
û(n)
=
h(n)
– ĥ(n),
û(n)≥0.
Из условия монотонности следует, что
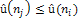 , т.е. недооценка h(n) в родительских вершинах больше или равно недооценкам h(n) в дочерних вершинах. На графе, изображенном на рисунке граф состояний с многократно раскрываемыми вершинами, условие монотонности не выполняется для начальной вершины. Например, h(S) > h(D) + c(S,D), т.е. 14 > 10 + 1. , т.е. недооценка h(n) в родительских вершинах больше или равно недооценкам h(n) в дочерних вершинах. На графе, изображенном на рисунке граф состояний с многократно раскрываемыми вершинами, условие монотонности не выполняется для начальной вершины. Например, h(S) > h(D) + c(S,D), т.е. 14 > 10 + 1.
Если ĥ(n) = h(n), то информированность является полной. В этом случает никакого поиска не происходит и приближение к цели идет по оптимальному пути.
Таким образом, свойства А-алгоритма существенно зависят от условий, которым удовлетворяет или не удовлетворяет эвристическая часть оценочной функции f(n):
-
А-алгоритм соответствует алгоритму равных цен, если h(n) = 0;
-
А-алгоритм гарантирует оптимальное решение, если ĥ(n) ≤ h(n); в этом случае он называется А* - алгоритмом;
-
А- алгоритм обеспечивает однократное раскрытие вершин, если выполняется условие монотонности
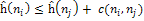 ; ;
-
Алгоритм
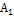 * эвристически более сильный, чем алгоритм * эвристически более сильный, чем алгоритм
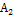 * при * при
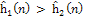 ; ;
-
А*- алгоритм полностью информирован, если ĥ(n) = h(n);
-
При ĥ(n) > h(n) А-алгоритм не гарантирует получение оптимального решения, однако часто решение получается быстро.
Рассмотренные алгоритмы поиска в пространстве состояний можно систематизировать с помощью таблицы.
|
Несис-темати-ческие |
Систематические |
|
Неинформированные |
Информированные |
|
Без оценки затрат |
С оценками затрат |
|
|
cписок OPEN – механизи «LIFO» |
cписок OPEN – механизи «FIFO» |
Стоимость от старта ĝ(n) |
Стоимость до цели ĥ(n) |
Стоимость от старта к цели
f(n)
= ĝ(n) + ĥ(n) |
|
Случайный поиск (Random) |
Поиск в глубину (Depth) |
Поиск вершин (Breadth) |
Алгоритм
равных
цен
(Optimal Search) |
Алгоритм подъема на гору (Hill
climbing) |
Глобальный учет соответствия цели (Best-First) |
|
ĥ(n) ≤ h(n)
А* - алгоритм |
|
|
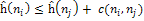
А* с ограничением монотонности |
Поиск решений в пространстве состояний может выполняться в нескольких направлениях: из начального состояния в целевое состояние (поиск, управляемый данными); из целевого состояния в начальное состояние (поиск, управляемый целью, или обратный поиск); одновременно в двух направлениях (комбинированный поиск). Так как поисковые графы (деревья) для практических задач велики, то двунаправленный поиск может быть эффективнее однонаправленного.
Поиск решений в пространстве состояний – комбинаторная задача. Решение получается на основе перебора всех состояний. Однако для многих практических задач полный перебор невозможен. Были предложены различные меры для оценки сложности решаемой задачи. Одна из них – это степень разветвления вершин графа состояния. Она равна среднему числу дочерних вершин, приходящихся на одно состояние задачи. Если рассматривать дерево состояний, то можно вывести формулу, устанавливающую зависимость общего числа состояний N от степени разветвления В и глубины дерева L:
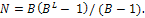
|


