Создаем искусственный интеллект. Урок 4. Поиск решений задач в пространстве состояний.

Эвристический поиск.

Основная идея эвристического поиска состоит в использовании дополнительной информации для управления процессом поиска. Эта дополнительная информация формируется на основе эмпирического опыта, догадок и интуиции исследователя, т.е. эвристик. Использование эвристик позволяет сократить количество просматриваемых вариантов при поиске решения задачи, что ведет к более быстрому достижению цели.

В алгоритмах эвристического поиска список открытых вершин упорядочивается по возрастанию некоторой оценочной функции, формируемой на основе эвристических правил. Оценочная функция может включать две составляющие, одна из которых называется эвристической и характеризует близость текущей и целевой вершин. Чем меньше значение эвристической составляющей оценочной функции, тем ближе рассматриваемая вершина к целевой вершине. В зависимости от способа формирования оценочной функции выделяют следующие алгоритмы эвристического поиска: алгоритм «подъема на гору», алгоритм глобального учета соответствия цели, А-алгоритм.

1. Алгоритм «подъема на гору». Алгоритм осуществляется целенаправленный поиск в направлении наибольшего убывания эвристической оценочной функции 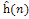. Данная функция обеспечивает оценку (прогноз) стоимости кратчайшего пути от текущей вершины n до ближайшей целевой вершины, т.е. является мерой стоимости оставшегося пути. Чем меньше значение 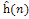,тем более «перспективен» путь, на котором находится вершина.

Подобный алгоритм используется при поиске экстремумов функции. Известно, что положение экстремума функции многих переменных определяется направлением вектора градиента функции. Поэтому поиск экстремума осуществляют в направлении наибольшего возрастания (убывания) функции, т.е. в направлении, совпадающем (или противоположном) с направлением градиента. Поиск максимума функции в этом случае напоминает восхождение на пик по наиболее крутому маршруту. Поэтому рассматриваемый алгоритм и называют алгоритмом «подъема на гору» (hill – climbing).

На очередном шаге алгоритма для каждой из дочерних вершин 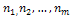 вершины вычисляется значение оценочной функции 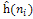, и для продолжения пути выбирается вершина с наименьшим значением 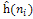. Процедура поиска терпит неудачу, если для всех дочерних вершин

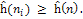
Procedure Hill_Climbing;
Begin
    n := ’начальная вершина’;
    While n <> ’целевая вершина’ Do Begin
    Раскрыть вершину n для всех дочерних вершин вычислить оценки ;
    Выбрать дочернюю вершину с минимальным значением ;
    If Then Выход(НЕУДАЧА);
        n := ;
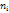    End;
    Выход(НЕУДАЧА);
End.

Существуют различные способы построения эвристической оценочной функции, однако готовых рецептов нет. При решении каждой конкретной задачи используют ранее накопленный опыт решения подобных задач. Оценка 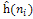вычисляться с помощью формулы:

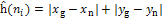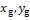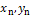где - координаты целевой вершины; - координаты текущей вершины.

Данная оценка соответствует расстоянию от вершины n до целевой вершины. При поиске пути в лабиринте, изображенном на рисунке Графы состояний,а, последовательность раскрываемых вершин будет следующей: A, B, L, G. Поиск пути в лабиринте, показанном на рисунке Графы состояний,б, завершится неудачей. При этом последовательность раскрытых вершин будет следующей: A, B. Оценочная функция 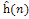в вершине В получит значение 3. Дальнейшие шаги оказываются безуспешными, так как ĥ(F)=3 и ĥ(C)=4, а для продолжения поиска необходимо, чтобы выполнялось условие

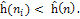
Таким образом, хотя данный алгоритм обеспечивает ускорение поиска, он не гарантирует достижение целевой вершины. Преждевременное завершение алгоритма происходит в следующих случаях: если в процессе поиска встречаются локальные минимумы оценочной функции ĥ(n); если для группы соседних вершин оценки ĥ(n) равны между собой (проблема «плато»).

2. Глобальный учет соответствия цели. Этот алгоритм поиска решения задачи похож на предыдущий. Здесь также оценивается «перспективность» того или иного пути с помощью эвристической оценочной функции ĥ(n). Отличие состоит в том, что на каждом этапе выполняется не локальное сравнение всех вершин-кандидатов, находящихся в списке OPEN. Для этого список открытых вершин сортируется в порядке возрастания значений ĥ(n).Наилучшая вершина для продолжения пути будет находиться на первом месте в списке OPEN. Поэтому данный алгоритм называют также алгоритмом выбора первой наилучшей вершины (Best-First).

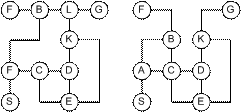
 а)                                   б)

Рисунок – Графы состояний.

Процедура поиска, основанная на данном алгоритме, похожа на процедуру Optimal_Search. Отличие состоит в том, что вместо функции стоимости ĝ(n) применяется эвристическая функция ĥ(n), т.е. учитываются только предстоящие затраты:

Procedure Best_First_Search;

Begin

    Поместить начальную вершину в список OPEN;

    CLOSED := ’пустой список’;

    While OPEN <> ’пустой список’ Do Begin

        n := first(OPEN);   

        If n = ’целевая вершина’ Then Выход(УСПЕХ);

        Переместить n из списка OPEN в CLOSED;

        Раскрыть вершину n, для каждой дочерней вершины вычислить ;

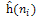        Поместить дочерние вершины, которых нет в списке OPEN и

        CLOSED, в список OPEN, связав с каждой вершиной указатель

        на вершину n;

        Упорядочить список OPEN по возрастанию значения ;

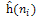    End;

    Выход(НЕУДАЧА);

End.

Если данную процедуру применить к задаче поиска пути в лабиринте, изображенном на рисунке Графы состояний,а, то результат будет таким же, как и в случае алгоритма подъема в гору. Если процедура Best_First_Search применить к лабиринту, представленному на рисунке Графы состояний,б, то состояние списка открытых вершин будет следующим:

 (S(6)) → (A(5)) → (B(3)C(4)) → (F(3)C(4)) → (C(4)) → (D(3)E(4)) → (K(2)E(4)) → (G(0)E(4)).

Таким образом, алгоритм позволяет успешно справляться с проблемой локальных минимумов. Однако при этом снижается эффективность самого процесса поиска. Эффективность процесса поиска будет оставаться высокой, если оценка стоимости кратчайшего пути ĥ(n) из вершины n в целевую вершину будет как можно ближе к реальной стоимости ĥ(n).