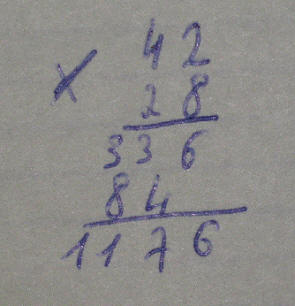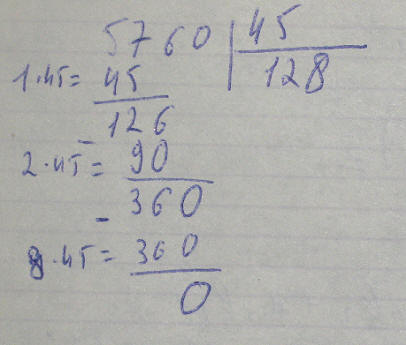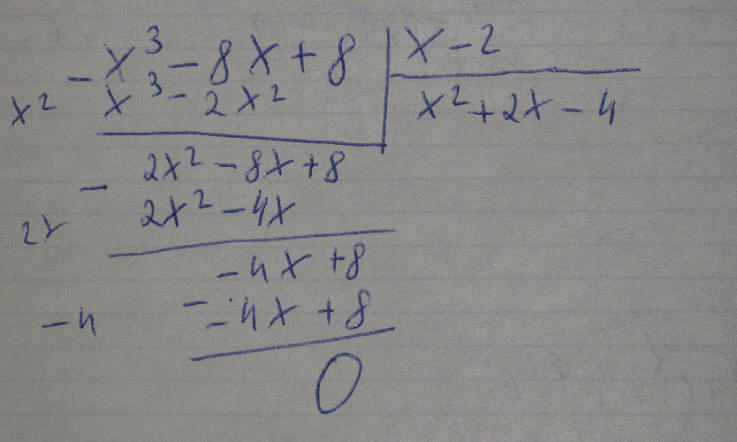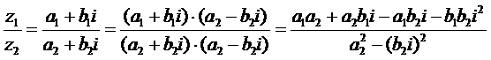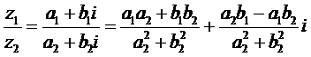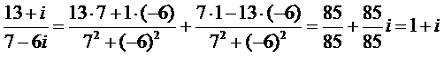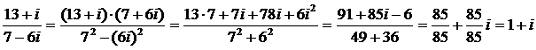| Комплексные числа для чайников. Урок 2. Алгебраическая форма комплексных чисел. |

|

|
| Автор megabax | |||||||||||||||||||||
| 11.03.2021 г. | |||||||||||||||||||||
Комплексные числа для чайников. Урок 2. Алгебраическая форма комплексных чисел.Это последний урок из серии "Комплексные числа для чайников", публикуемый в бесплатном разделе. Начиная со следующего, публикация уроков будет продолжена в платном разделе. В бесплатном же разделе, возможно, иногда будут публиковать некоторые статьи, посвященные особенностям математики комплексных чисел . Продолжаем знакомство с комплексными числами. На прошлом уроке мы с вами рассмотрели, что такое абстракция в математике, для чего нам нужны абстракции в повседневной жизни а так же узнали об еще одной абстракции - мнимой единице. Так же я привел вам список областей, где эти самые комплексные числа могу применятся и обещал, что со временем, читая мои уроки вы поймете тайный смысл мнимой единицы. И так, продолжим. Алгебраическая запись комплексного числа. Она выражается вот такой формулой:
где a и b - некоторые числа, i - мнимая единица. Разумеется, можно записать и так:
Но принято записывать как в формуле (2.1), обозначая мнимую единицу символом i. Что можно делать с такими числам? Во первых, их можно складывать. Для этого достаточно сложить их коэффициенты:
Собственно говоря, сложение комплексный чисел - это тоже самое, что и сложение многочленов. По своей сути - комплексное число - это многочлен, состоящий из двух членов (двучлен). Если вы подзабыли алгебру, немножко напомню. Давайте представим, что мы считаем яблоки. У нас на одной полке лежит три яблока, на другой четыре. В сумме 7. Но что, если у нас на одной полке три яблока, а на другой четыре апельсина? Можем ли мы их сложить и сказать, что у нас семь яблокапельсинов? Разумеется, нет, такая операция лишена всякого смысла. Но мы можем сказать, что у нас три яблока плюс четыре апельсина. Это и есть многочлен. И, если мы одно яблоко обозначим буквой X, а другое буквой Y, то у нас получиться 3X+4Y. Теперь заменим яблоки и апельсины коробками с конфетами. Пусть у нас имеются три больших коробки, и две маленьких. В этих коробках разное количество конфет. Поэтому мы не можем взять и сложить коробки друг с другом. Но мы можем количество конфет в большой коробке обозначить X, а в маленькой Y. Тогда общее количество конфет у нас будет 3X+2Y. Узнав, сколько конфет в каждой коробке мы можем сосчитать их по полученной формуле. А пока не знаем, у нас конфет 3X+2Y. А теперь представим, что у нас имеется некоторое количество шоколадных конфет "россыпью" и некаторе количество мармелада в коробке. Обозначим одну коробку как i, а одну шоколадную конфету как a. Количество коробок с мармеладками обозначим b. Тогда у нас получиться a+bi. Это тоже многочлен. Если у нас есть несколько полок, где лежат и шоколадные конфеты и коробки с мармеладом, то содержимое этих полок мы можем складывать, как в формуле (2.3). Еще комплексные числа можно вычитать. Это тоже самое, что и в формуле (2.3), только вместо плюса между коэффициента знак минус, думаю, понятно, почему:
Теперь рассмотрим пример. Сложить комплексные числа 5-2i и 7+4i. Решаем: 5-2i+7+4i=12+2i. Обратите внимание, что в первом слагаемом перед i знак минус, а прибавления числа с минусом - это вычитание. Поэтому в итоге перед i остается 2, так как 4-2=2. Комплексные числа можно так же умножать друг на друга (формула не окончательна, ниже мы ее преобразуем):
Как вы поняли, перемножаются они точно так же, как и многочлены. Их произведение представляет собой произведение всех членов со всеми другими членами. Может возникнуть вопрос: а как вообще можно перемножить многочлены? Как умножить 5 апельсинов плюс 10 мандаринов на 3 шоколадки плюс 4 мармеладки? Что бы понять это, вспомним школьную арифметику. Помните как в школе вас учили складывать и умножать столбиком? Не знаю, может сейчас этому уже не учат, так как есть калькуляторы. Но во времена моего детства калькуляторы были в диковинку и мы арифметические операции производили на бумаге, тем самым пресловутым "столбиком". Если вы это не помните или не проходили, напомню:
И так, на картинке мы видим умножение 42 на 28. Как мы это делаем? В пером ряду, там где у нас 336, мы умножаем 8 на 42. Во втором, где у нас цифры "84", мы 42 умножаем на 2. Но на самом деле мы не 42 умножаем на 2, а 42 на 20, и получается у нас не 84, а 840, просто мы не пишем последний нуль. Иными словами, умножение 42 на 28 мы можем представить в таком виде: 42*28=(42*8+42*20). Если не верите, проверьте на калькуляторе :). Но это еще не все. Умножение 42*8 мы тоже можем разложить таким же макаром, как, впрочем, и 42*20. Вот что тогда у нас получается: 40*8+2*8+40*20+2*20. Но, на самом деле, 42 - это 40+2, а 28 - это 20+8. И мы можем записать (40+2)*(20+8). Если мы раскроем скобки, то получим такой же результат. Заменив цифры буквами, мы получим вот такую универсальную формулу:
Но откуда взялась такая формула? Что бы понять, попробуем сначала выражение c+d умножить на a. У нас получается ac+ad. Почему? Потому что мы берем c+d число раз, которое у нас обозначается буквой a. Если а=5, то мы пять раз возьмем число c+d. Так как от перестановки слагаемых сумма не меняется (это настолько очевидно, что думаю, объяснения излишни), то не важно, вместе или по отдельности мы взяли пять раз c и d. Таким образом, 5*(c+d)=5c+5d. Тоже самое справедливо, когда мы умножаем на a. Но в формуле (2.7) у мы раскрываем таким же макаром два выражения в скобках. Поэтому и получается, что каждый член многочлена умножается на каждый другой член многочлена и полученные произведения складываются. А теперь посмотрим внимательно на формулу (2.5). Что вам сразу бросается в глаза? Правильно, i в квадрате, которое, по сути, равно -1, и два члена с i, которые можно объединить. Тогда формула приобретает такой вид:
В дальнейшем вы еще не раз столкнетесь с "хитрыми" свойствами комплексных чисел, вытекающих из самого понятия мнимой единицы. А сейчас изучим .... деление комплексных чисел. Взрыв мозга, не правда ли? Как можно делить друг на друга комплексные числа? Как вообще можно делить друг на друга многочлены? А точно так же, как и умножать. Уголком! Вот, посмотрите процесс деления двух числе в десятичной системе:
Как вы уже поняли ранее, числа можно представить как многочлены. Так, 5760=5000+700+60+0=5•103+7•102+6•10+0. Да и 45 тоже можно представить как многочлен 4•10+5. Давайте рассмотрим пример деления многочлена:
Разумеется, как числа в десятичной системе счисления, так и многочлены могут на цело не разделится. Комплексные числа - это, по сути, тоже многочлены, и их можно делить друг на друга. Но тут есть один нюанс. И он опять же связан с "хитрым" свойством мнимой единицы. И так, сначала вспомним древнюю бородатую формулу, которую проходили еще в начальных классах:
Откуда взялась эта формула, объяснять, думаю, излишне, тут рули Капитан Очевидность. Но если вы такой дотошный, сами попробуете вывести эту формулу из формулы (2.7). Как вы уже поняли, квадраты - лучшие друзья мнимой единицы, так как превращают ее из какой то непонятной абстракции в нормальное число, тем самым облегчая нам расчеты. Это один из тайных смыслов мнимой единицы и сейчас вы в этом убедитесь. И так, берем два комплексны числа и делим их. Для того, что бы их разделить, умножаем его числитель и знаменатель, который позволит нам раскрыть скобки и избавиться от дроби:
Как вы поняли, мы помножили на второй многочлен из формулы (2.9), что бы в знаменателе у нас получилась разность квадратов. Что это нам дает? А то, что i будет в квадрате, а это минус единица. И мы избавляемся от комплексно составляющей в знаменателе, то есть, теперь мы будем делить уже на самое обычно число:
Кому то эта формула покажется страшноватой, но не бойтесь, учить ее не надо. В любом случае, вы можете и без нее подобрать множитель, который превратит знаменатель в разность квадратов. Рассмотрим пример:
В данном примере мы сосчитали по формуле (2.11). А сейчас посмотрите, как это можно сделать без формулы:
Кто то, возможно, спросить: а можно ли делить комплексные числа "уголком", как многочлен? Попытаться можно. Но вряд ли у вас что то получиться. Многочлен 13+i не разделиться нацело на 7-6i. Более того, вы будете долго мучиться с таким делением, но так и ничего не разделите. И, только преобразуя квадрат от i минус единицу, вы получаете "красивый" результат. Правда, кому то может быть непонятно, а в чем практической польза от таким манипуляций? Дело в том, что комплексные числа, кроме алгебраической, могут быть так же представлены в тригонометрической и даже экспоненциальной форме. Их можно преобразовывать из одной формы в другую, и такие преобразования находят применение во многих практических расчетах из разных областей науки и техники. Но об этом в будущих уроках. Оставайтесь с нами.
|
|||||||||||||||||||||
| Пред. » |
|---|