Теория вероятностей и математическая статистика. Урок 3. Повторные испытания

Автор megabax

10.03.2021 г.

New Page 1

Теория вероятностей и математическая статистика. Урок 3. Повторные испытания

Отдельного рассмотрения заслуживают так называемые повторные испытания. Повторные испытания - это испытания, которые проводятся в одних и тех же условиях независимо друг от друга с постоянной вероятностью успеха в каждом. Классический пример повторных испытаний - бросание игральной кости или вращение рулетки в казино. Кстати, о казино. Некоторые думают, что существует такая стратегия, которая позволяет выигрывать у казино. Так вот, изучение повторных испытаний как раз таки даст ответ на вопрос, существует ли подобная стратегия и если да, то что же это за такая стратегия.

Если испытание имеет два независимых исхода, то его можно описать формулой Бернулли. Пусть, например, стрелок стреляет по мишени. Вероятность попадания равна p, а вероятность, что он промажет q. Естественно, p=1-q. Предположим, он стреляет по 10-ти мишеням и у него есть 10 выстрелов. Каковая вероятность того, что будет поражено ровно три мишени?

Для начала определим вероятность одной из возможных комбинаций, например, три пораженных мишени - это первые три мишени. Вероятность такого случая будет равна pppqqqqqqq=p³q⁷. Но у нас могут быть и такие комбинации: ppqpqqqqqq=p³q⁷, и такие ppqqpqqqqq=p³q⁷, и еще много разных сочетаний, вероятность которых будет p³q⁷ , так от перестановки множителей произведение не меняется. Таким образом, для определения вероятности нам надо умножить количество сочетаний трех из семи умножить на p³q⁷:

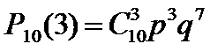
Для общего случая справедлива так называемая формула Бернулли:

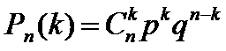(3.1)

где n -число испытаний, k - количество успешных испытаний.

Пример 1. Какова вероятность, что если бросить игральную кость 5 раз, ровно один раз выпадет число 3. Каковая вероятность, что число 3 выпадет ровно два раза.

Решение. Вероятность выпадения числа 3 равно 1/6. Используя формулу (3.1), вычисляем (размещение считается по формуле (1.4) из урока 1):

Теория вероятностей и математическая статистика. Урок 3. Повторные испытания

Пример 2. Студен упорно не желает учить билеты и собирается сдать экзамен наобум. Но все таки 3 из 10 билетов он выучил. На экзамене выдается 2 билета. Экзамен считается сдан на удовлетворительную оценку, если студент правильно ответил хотя бы на один билет. Какова вероятность что студент сдаст экзамен, если дается три попытки?

Решение. Для начала нам надо вычислить вероятность, что студент сдаст экзамен с одной попытки. Так как он упорно не желает учить билеты, кроме тех трех, что уже выучил, в каждой из трех попыток у нас будет одинаковая вероятность сдать экзамен.

Итак, вероятность того, что студент вытащит первый билет, ответ на который он знает, равна 0.3. Но какова вероятность того, что если студент вытащит два билета, хотя бы один из них окажется "счастливым"? Эта вероятность равна единица минус вероятность того, что оба билета окажутся "несчастливыми". Она равна

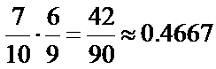
Значит, вероятность сдать с первой попытки равна 0.5333. Каковая вероятность сдать экзамен, когда дано три попытки? В данном случае мы лучше посчитаем, какова вероятность провались экзамен, а вероятность сдать равна единица минус вероятность провалить. Таким образом:

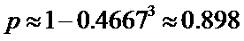
Как видим, у халявщика неплохие шансы сдать экзамен. К счастью, обычно бывает больше 10 билетов, так что, вероятность случайного прохождения таких горе студентов гораздо меньше.

Пример 3. Неопытный стрелок стреляет в тире. Вероятность того, что он попадет по мишени, равна всего 5%. Но для того, чтобы получить приз, достаточно попасть по мишени хотя бы 3 раза из 20. Оценить шансы стрелка выиграть приз.

Решение. Для решение данной задачи нам удобнее всего вычислить вероятность того, что стрелок не поразит нужно количество мишеней. Этот случай наступает тогда, когда количество пораженных мишеней ровно 2, ровно 1 и ровно ни одной. Вероятность того, что стрелок не выиграет равна сумме вероятностей перечисленных количество попаданий. Для вычисления, сколько раз стрелок попадет в мишень (кроме случая "ни одного раза"), мы можем воспользоваться формулой Бернулли (3.1):

Итак, мы вычислили вероятность того, что стрелок поразит ровно 1 и ровно 2 мишени. Осталось вычислить вероятность того, что он не поразит ни одной мишени. Она равна:

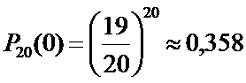
Суммируя эти вероятности, мы получим вероятность того, что стрелок поразит мишень менее трех раз:

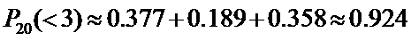
Таким образом, вероятность того, что стрелок поразит не менее трех мишеней, равна 1-0.924=0.076 (всего 7.6%). Кому то такой результат покажется странным. Давайте проверим. Вычислим вероятность того, что стрелок поразит ровно три мишени. Результат должен быть меньше чем 7.6%.:

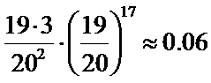
Пример 4. На 10000 изделий в приходиться среднем приходить 15 бракованных. Какова вероятность, что в партии из 1000 изделий ровно два окажутся бракованные?

Решение. Если мы применим формулу Бернулли (3.1) то получим очень плохо вычислимое выражение:

В данном случае мы, конечно, можем прибегнуть к сокращению:

Но не всегда нам удастся решить выражение так относительно легко. Если нам надо будет найти вероятность того, что бракованных деталей не 2, а, допустим, 20? Тут мы уже столкнемся с большими, буквально "астрономическими" числами при вычислении факториалов. И, более того, мы не сможем вычислить их при помощи калькулятора. но существует и другая формула вычисления такой вероятности, формула Пуассона:

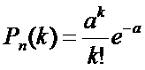(3.2)

где a=np. Для нашего случая a=1000∙15/10000=1.5. Вычисляем:

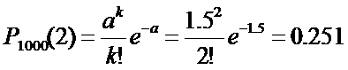
Однако, при очень больших n и вероятности успеха в отдельных испытаниях больше 0.1, формула Пуассона дает весьма неточный результат. В этом случае целесообразно использовать формулу Муавра-Лапласса:

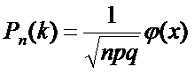(3.3)

где φ(x) так называемая нормальная функция, которая вычисляется по формуле:

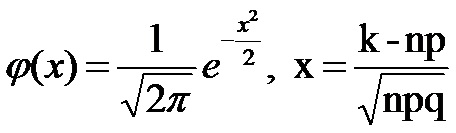(3.4)

Пример 4. Пусть в зале 150 человек. Какова вероятность, что ровно треть из них (50 человек) родилась летом, если предположить, что вероятность родиться в тот или иной сезон распределяется равномерно по году и равна 1/4 (25%).

Решение. В данном случае, определения даты рождения каждого человека можно считать испытанием. Количество испытаний - это число людей, сидящих в зале, а количество удачных испытаний - это количество случаев, когда выполниться условия: дата рождения выпадает на лето. Воспользуемся формулой Муавра-Лапалсса (3.3). Для начала вычислим x по формуле (3.4):

Теперь вычислим φ(x):

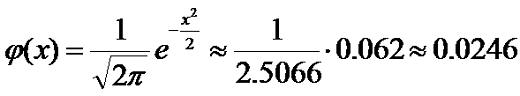
Теперь мы можем вычислить вероятность:

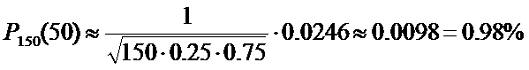
Однако, в большинстве задач требуется вычислить вероятность не для какого-то определенного количества, а для диапазона. В этом случае необходимо воспользоваться интегральной формулой Муавра-Лапласса:

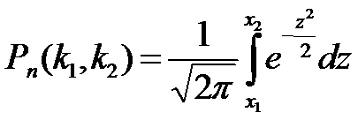(3.5)

где x₁ и x₂ вычисляются по формулам:

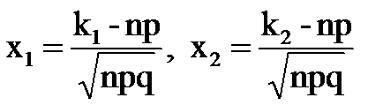(3.6)

Этот интеграл относиться к разряду "не берущихся", то есть, тех, которые не имеют аналитического решения, поэтому для вычисления используют так называемую функцию Лапласса:

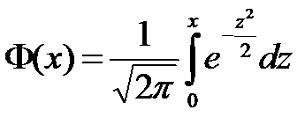(3.7)

На практике значения этой функции берут из таблицы функции Лапласса

x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)	x	Ф(x)
0,00	0,00000	0,50	0,19146	1,00	0,34134	1,50	0,43319	2,00	0,47725	3,00	0,49865
0,01	0,00399	0,51	0,19497	1,01	0,34375	1,51	0,43448	2,02	0,47831	3,05	0,49886
0,02	0,00798	0,52	0,19847	1,02	0,34614	1,52	0,43574	2,04	0,47932	3,10	0,49903
0,03	0,01197	0,53	0,20194	1,03	0,34849	1,53	0,43699	2,06	0,48030	3,15	0,49918
0,04	0,01595	0,54	0,20540	1,04	0,35083	1,54	0,43822	2,08	0,48124	3,20	0,49931
0,05	0,01994	0,55	0,20884	1,05	0,35314	1,55	0,43943	2,10	0,48214	3,25	0,49942
0,06	0,02392	0,56	0,21226	1,06	0,35543	1,56	0,44062	2,12	0,48300	3,30	0,49952
0,07	0,02790	0,57	0,21566	1,07	0,35769	1,57	0,44179	2,14	0,48382	3,35	0,49960
0,08	0,03188	0,58	0,21904	1,08	0,35993	1,58	0,44295	2,16	0,48461	3,40	0,49966
0,09	0,03586	0,59	0,22240	1,09	0,36214	1,59	0,44408	2,18	0,48537	3,45	0,49972
0,10	0,03983	0,60	0,22575	1,10	0,36433	1,60	0,44520	2,20	0,48610	3,50	0,49977
0,11	0,04380	0,61	0,22907	1,11	0,36650	1,61	0,44630	2,22	0,48679	3,55	0,49981
0,12	0,04776	0,62	0,23237	1,12	0,36864	1,62	0,44738	2,24	0,48745	3,60	0,49984
0,13	0,05172	0,63	0,23565	1,13	0,37076	1,63	0,44845	2,26	0,48809	3,65	0,49987
0,14	0,05567	0,64	0,23891	1,14	0,37286	1,64	0,44950	2,28	0,48870	3,70	0,49989
0,15	0,05962	0,65	0,24215	1,15	0,37493	1,65	0,45053	2,30	0,48928	3,75	0,49991
0,16	0,06356	0,66	0,24537	1,16	0,37698	1,66	0,45154	2,32	0,48983	3,80	0,49993
0,17	0,06749	0,67	0,24857	1,17	0,37900	1,67	0,45254	2,34	0,49036	3,85	0,49994
0,18	0,07142	0,68	0,25175	1,18	0,38100	1,68	0,45352	2,36	0,49086	3,90	0,49995
0,19	0,07535	0,69	0,25490	1,19	0,38298	1,69	0,45449	2,38	0,49134	3,95	0,49996
0,20	0,07926	0,70	0,25804	1,20	0,38493	1,70	0,45543	2,40	0,49180	4,00	0,49997
0,21	0,08317	0,71	0,26115	1,21	0,38686	1,71	0,45637	2,42	0,49224	4,05	0,49997
0,22	0,08706	0,72	0,26424	1,22	0,38877	1,72	0,45728	2,44	0,49266	4,10	0,49998
0,23	0,09095	0,73	0,26730	1,23	0,39065	1,73	0,45818	2,46	0,49305	4,15	0,49998
0,24	0,09483	0,74	0,27035	1,24	0,39251	1,74	0,45907	2,48	0,49343	4,20	0,49999
0,25	0,09871	0,75	0,27337	1,25	0,39435	1,75	0,45994	2,50	0,49379	4,25	0,49999
0,26	0,10257	0,76	0,27637	1,26	0,39617	1,76	0,46080	2,52	0,49413	4,30	0,49999
0,27	0,10642	0,77	0,27935	1,27	0,39796	1,77	0,46164	2,54	0,49446	4,35	0,49999
0,28	0,11026	0,78	0,28230	1,28	0,39973	1,78	0,46246	2,56	0,49477	4,40	0,49999
0,29	0,11409	0,79	0,28524	1,29	0,40147	1,79	0,46327	2,58	0,49506	4,45	0,50000
0,30	0,11791	0,80	0,28814	1,30	0,40320	1,80	0,46407	2,60	0,49534	4,50	0,50000
0,31	0,12172	0,81	0,29103	1,31	0,40490	1,81	0,46485	2,62	0,49560	4,55	0,50000
0,32	0,12552	0,82	0,29389	1,32	0,40658	1,82	0,46562	2,64	0,49585	4,60	0,50000
0,33	0,12930	0,83	0,29673	1,33	0,40824	1,83	0,46638	2,66	0,49609	4,65	0,50000
0,34	0,13307	0,84	0,29955	1,34	0,40988	1,84	0,46712	2,68	0,49632	4,70	0,50000
0,35	0,13683	0,85	0,30234	1,35	0,41149	1,85	0,46784	2,70	0,49653	4,75	0,50000
0,36	0,14058	0,86	0,30511	1,36	0,41309	1,86	0,46856	2,72	0,49674	4,80	0,50000
0,37	0,14431	0,87	0,30785	1,37	0,41466	1,87	0,46926	2,74	0,49693	4,85	0,50000
0,38	0,14803	0,88	0,31057	1,38	0,41621	1,88	0,46995	2,76	0,49711	4,90	0,50000
0,39	0,15173	0,89	0,31327	1,39	0,41774	1,89	0,47062	2,78	0,49728	4,95	0,50000
0,40	0,15542	0,90	0,31594	1,40	0,41924	1,90	0,47128	2,80	0,49744	5,00	0,50000
0,41	0,15910	0,91	0,31859	1,41	0,42073	1,91	0,47193	2,82	0,49760
0,42	0,16276	0,92	0,32121	1,42	0,42220	1,92	0,47257	2,84	0,49774
0,43	0,16640	0,93	0,32381	1,43	0,42364	1,93	0,47320	2,86	0,49788
0,44	0,17003	0,94	0,32639	1,44	0,42507	1,94	0,47381	2,88	0,49801
0,45	0,17364	0,95	0,32894	1,45	0,42647	1,95	0,47441	2,90	0,49813
0,46	0,17724	0,96	0,33147	1,46	0,42785	1,96	0,47500	2,92	0,49825
0,47	0,18082	0,97	0,33398	1,47	0,42922	1,97	0,47558	2,94	0,49836
0,48	0,18439	0,98	0,33646	1,48	0,43056	1,98	0,47615	2,96	0,49846
0,49	0,18793	0,99	0,33891	1,49	0,43189	1,99	0,47670	2,98	0,49856

Вероятность попадания в диапазон будет разностью этих двух значений функции.

Пример 5. Условие такие, как и в примере 4, но надо определить, какова вероятность, что от 40 до 60 человек из сидящих в зале родились летом.

Решение. Нижнее значение диапазона - 40, верхнее - 60 (количество сидящих в зале). Вычисляем:

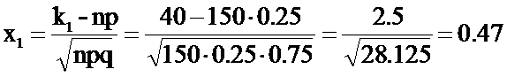
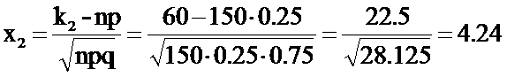
Значения функции Лапласа для этих x 0.18082 и 0.49999 соответственно. Вычитаем из верхнего порога нижний и получаем p_n(40,60)=0.49999-0.18082=0.31917≈31%

Пред. »

Вернуться