New Page 1
Теория вероятностей и математическая
статистика. Урок
2. Основные аксиомы и теоремы
Аксиома 1. Вероятность двух несовместных событий равна
сумме вероятностей этих событий:
|
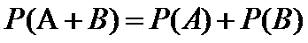 |
(2.1) |
Формула верна для любого количества событий, причем,
вероятность суммы событий, составляющих полную группу событий, равна единице. В
частном случае, для противоположных событий справедлива формула:
|
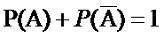 |
(2.2) |
Отсюда следует вероятность противоположного события:
|
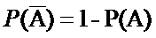 |
(2.3) |
Во многих случаях удобнее обозначать вероятности
противоположных событий буквами p и
q, где
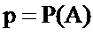
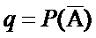
Тогда:
|
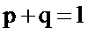 |
(2.4) |
Пример 1. Каткова вероятность, что на игральной кости
выпадет более двух очков?
Решение. При бросании игральной кости возможны шесть
событий от A1 до A6.
Все эти события несовместны. Событию "выпадет больше двух очков"
соответствуют любое из событий A3,
A4, A5,
A6. Вероятность каждого из событий
1/6, поэтому:
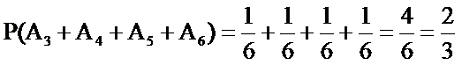
Теперь разберем такое понятие, как произведение совместных
событий. Под произведением событий A и
B (AB) мы понимаем такую ситуацию, когда произошло
событие A, а затем событие B.
Вероятность произведения событий AB равна
произведению вероятности события A на условную
вероятность события B. Под условной вероятностью
события B подразумевается вероятность наступления
события B при условии, что событие
A наступило.
Если наступление события A изменяет
условие наступления события A, то такие события
называют зависимыми. В противном случае события независимы и
условная вероятность равна безусловной. Условную вероятность события
B обозначают P(B|A). Тогда:
|
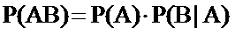 |
(2.5) |
При этом справедливо равенство:
|
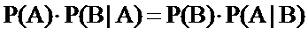 |
(2.6) |
Для независимых событий, когда условная и безусловная
вероятность равны, вероятность совместного события AB
находиться по формуле:
|
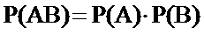 |
(2.7) |
Пример 2. Из урны, в которой 10 желтых и 5 красных
шаров извлекают по очереди два шара. Какова вероятность извлечь последовательно
сначала красный, а потом желтый шар, если:
1) Первый извлеченный шар возвращают обратно.
2) Первый извлеченный шар обратно не возвращают.
Решение. Событие "извлекли красный шар"
обозначили A, "извлекли желтый шар" обозначим
B. В первом случае эти события независимы, так как мы
шар возвращаем обратно и поэтому вероятность извлечь шар заданного цвета не
меняется. Тогда:
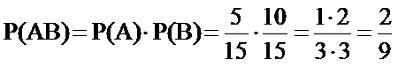
Во втором случае события будут уже зависимые, то есть, после того, как мы
извлеки красный шар, вероятность извлечения желтого шара поменяется, то есть:
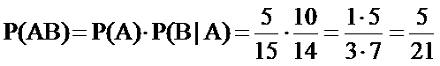
Если у нас имеет место случай, когда надо вычислить вероятность двух
совместных событий, то применим следующую формулу:
|
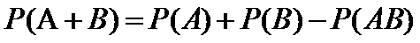 |
(2.8) |
Для понимания, что значит вероятность двух совместных
событий, рассмотрим пример.
Пример 3. Двое снайперов стреляют по мишени по одному
разу. Первый из них стреляет лучше и вероятность, что он попадет в цель, равна
0.9, а второй - мазила, вероятность что он попадет в цель 0.5. Цель считается
пораженной, если хот кто-нибудь из них попадет ну, или попадут оба.
Решение. По формуле 2.8 вычислим вероятность данного
события:
Эту задачу также можно решить и другим путем. Найдем вероятность того, что
оба промахнуться:
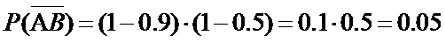
Тогда вероятность что хоть один из них не промахнется (цель будет поражена)
равняется:
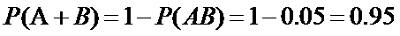
Пример 4. Игральная кость бросается 4 раза. Какова вероятность, что
хотя бы один раз выпадет число 3.
Решение. Вероятность того, что выпадет число 3 равна 1/6, что не
выпадет 5/6. Тогда искомая вероятность:
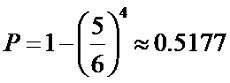
Теперь разберем такое понятие, как формула полной вероятности. Допустим,
некоторое событие A может произойти только в
результате наступления одного из случайных событий H1,H2,...,Hn,
которые составляют полную группу событий. Будем называть эти
события гипотезами с известными вероятностями их осуществления
P(H1),P(H2),...,P(Hn).
Тогда безусловную вероятность события A можно
найти по формуле полной вероятности, определяемой как сумма произведений
вероятностей гипотез на условные вероятностей события A:
|
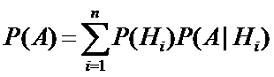 |
(2.9) |
Пример 5. В урне лежит 4 синий и 5 красных шаров. Из нее достали один
шар, цвет которого неизвестен. Затем достали второй. Какова вероятность, что
этот второй шар оказался синий?
Решение. Рассмотрим две гипотезы: H1
- первый шар синий, H2 - первый ша красный.
Вероятности этих гипотез
P(H1)=4/9,
P(H2)=5/9. Условные вероятности событий:
P(A|H1)=3/8,
P(A|H2)=4/8.
Тогда:
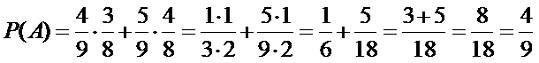
Представим себе, что событие в примере 5 произошло. Требуется
найти вероятность того, что реализовалась гипотеза
Hi. Из равенства 2.6 выводим так называемую
формулу Байеса.
Для нашего случая
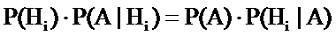
|
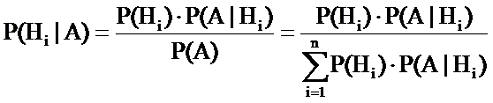 |
(2.10) |
Пример 6. Предположим, в предыдущем примере (5), оказалось, что второй
шар синий. Найти после опытную вероятность того, что первый шар тоже был синий.
Решение. По формуле Байеса находим:
Как видим, вероятность того, что это был синий шар, уменьшилась.
|


