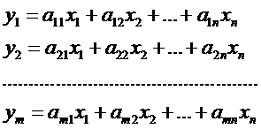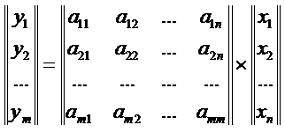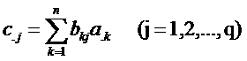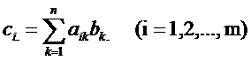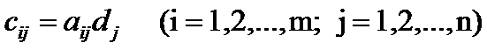| Матричное исчисление для чайников. Урок 3. Свойства действий над матрицами. |

|

|
| Автор megabax | |||||||||||||
| 08.03.2021 г. | |||||||||||||
Матричное исчисление для чайников. Урок 3. Свойства действий над матрицами.Это последний урок из серии "Матричное исчисление для чайников", публикуемый в бесплатном разделе. Начиная со следующего, публикация уроков будет продолжена в платном разделе. В бесплатном же разделе, возможно, иногда будут публиковать некоторые статьи, посвященные особенностям матричного исчисления. На прошлом уроке мы разобрали сложения и умножения матриц. Сегодня рассмотрим свойства таких действий. Как я говорил на прошлом уроке, закон "от перестановки множителей произведение не меняется" для матриц НЕ действует. Но вот что касается сложения, то тут правило перестановки прекрасно работает, то есть, для любых матриц A И B, которые можно складывать (которые имеют одинаковый размер), справедливо равенство: A+B=B+A Для матриц также существует сочетательный и распределительный закон, то есть: (AB)C=A(BC) (A+B)C=AC+AB A(B+C)=AB+AC Как следствие, общий множитель для нескольких слагаемых можно вынести за скобку, при условии, что соблюдается порядок перемножения. Например, можно так: AX+BX+SX=(A+B+S)X. Но если у нас вот такой многочлен AX+XB+SX то так делать уже нельзя, можно только вот так: AX+XB+SX=(A+S)X+XB. Линейное преобразование: Можно записать вот таким матричным равенством: Или, в сокращенном виде Y=AX, где X=(x1,x2,...,xn), Y=(y1,y2,...,yn), A - прямоугольная матрица размером m x n. Эти равенства могут быть записаны вот в таком виде:
или
Таким образом, любой j-ый столбец матрицы-произведения C=AB является линейной комбинацией столбцов первого сомножителя, то есть матрицы A, причем, коэффициенты этой линейной зависимости образуют j-ый столбец во втором сомножителе B. Аналогично, любая i-а строка в матрице C является линейной комбинацией строк матрицы B, коэффициентами этой линейной зависимости являются элементы i-ой строки матрицы A. Отсюда следуют следующие следствия. Следствие 1. Пусть у нас есть матричное уравнение
AX=C, где A и
X - матрицы, заданные соответственно
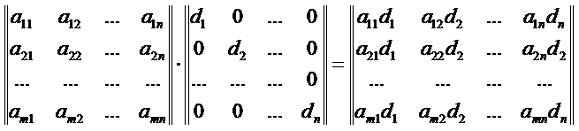
Следствие 2. Для уравнения XB=C необходимым и достаточным условием существование решения является то, что строки матрицы C являются линейными комбинациями строк матрицы B. Теперь рассмотрим один частный случай, когда в произведении C=AB второй сомножитель является квадратной, и при этом, еще и диагональной матрицей. Пусть диагональная матрица B={d1,d2,d3,...dn}. Тогда из формулы (2.12) урока 2 следует:
или
Если меняем множители местами, то:
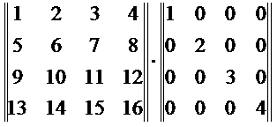
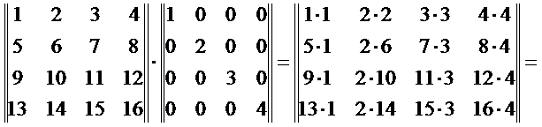
Таким образом, при умножении на диагональную матрицу мы просто умножаем каждый член умножаемой матрицы на элемент диагональной матрицы соответствующего столбца. То есть, весь первый столбец результатирующей матрицы - это произведение столбца первой матрицы на d1, второй d2, и так далее. Если мы наоборот, умножаем диагональную матрицу на другую матрицу, то наоборот, у нас идет умножение по строкам: каждый элемент первой строки умножается на d1, второй d2, и так далее. Рассмотрим пример. Вычислить произведение матриц Используя формулу (3.4), получаем:
|
|||||||||||||
| Последнее обновление ( 08.03.2021 г. ) | |||||||||||||
| Пред. » |
|---|