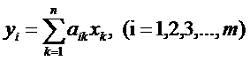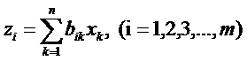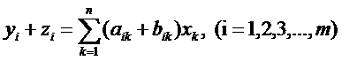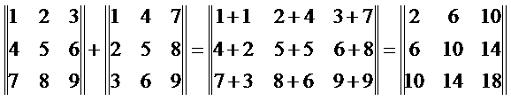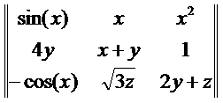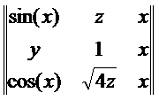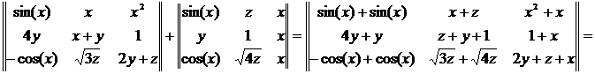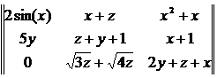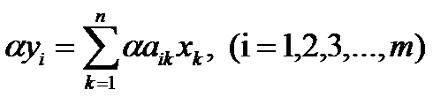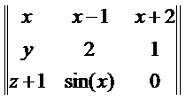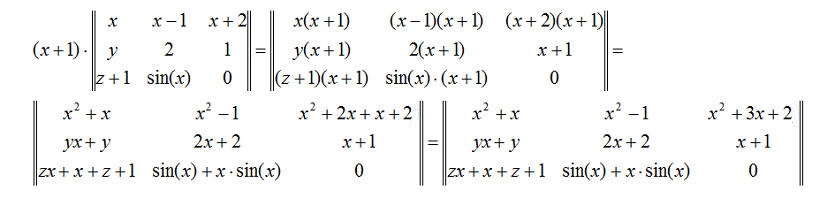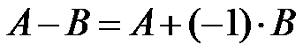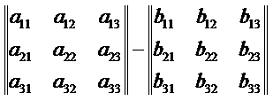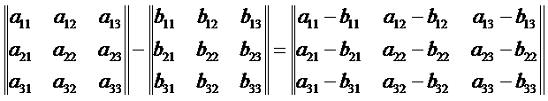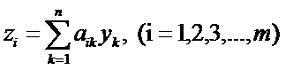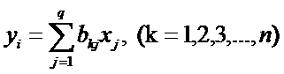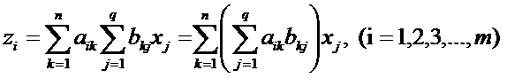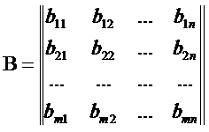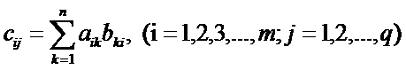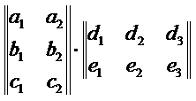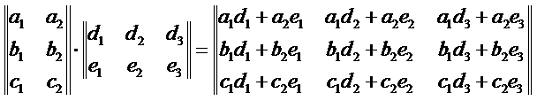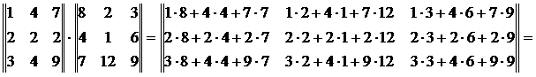Матричное исчисление для чайников. Урок 2. Сложение и умножение прямоугольных матриц.

В самом конце прошлого урока мы затронули тему линейных преобразований. Вспомним его. Пусть у нас есть некоторые числа y₁, y₂, ... y_m и числа x₁, x₂, ... x_m, между которыми существует зависимость:

Как вы помните, это и ест линейное преобразование. Пусть у нас также есть преобразование чисел z₁, z₂, ... z_m через те же числа x₁, x₂, ... x_m:

(2.2)

Тогда сумма чисел y₁, y₂, ... y_m и z₁, z₂, ... z_m будет выглядеть так:

Из прошлого урока (самый конец) мы помним, что то, что у нас в выражение (2.1) - это матрица. То, что в (2.2) - это тоже матрица. Таким образом, формула (2.3) наглядно показывает, что матрицы можно складывать. При этом получается матрица, которая содержит суммы соответствующих элементов слагаемы матриц. То есть, чтобы сложить матрицы, нам надо в каждой строчке сложить первые элементы, потом вторы и так до конца строки. Разумеется, складывать мы можем только матрицы одинакового размера (и по горизонтали, и по вертикали).

А теперь рассмотри научное определение сложения матриц. Суммой двух прямоугольных матриц и одинаковых размеров называется матрица , элементы которой равны сумме соответствующих элементов данных матриц:

если

(2.5)

Операция нахождения сумму матриц называется сложением матриц.

Пример 1. Найти сумму матриц:

и

Решение. Складываем соответствующие элементы матриц, получаем:

Пример 2. Найти сумму матриц:

и

Решение. Складываем соответствующие элементы матриц, получаем:

Сложение матриц обладает рядом свойств, которые следуют из определения:

• Переместительное свойство: A+B=B+A, где A и B - прямоугольные матрицы одинакового размера.

• Сочетательное свойство: (A+B)+C=A+(B+C), где A, B и C - матрица одинакового размера.

Мы рассмотрели операцию суммирования матриц. Теперь рассмотрим операцию умножения матрицы на коэффициент. Выполним умножения выражения (2.1) на некий коэффициент α из числового поля K:

исходя из данного выражения, имеем определения умножения матрицы на коэффициент: произведением матрицы на число α из числового поля K называется матрица , элементы которой получаются из соответствующих элементов матрицы A путем умножения на число α

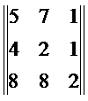
Пример 3. Умножим на 3 матрицу:

Решение:

Пример 4. Умножим на x+1 матрицу:

Решение:

Произведение матрицы на число обладает следующими свойствами:

• α(A+B)=αA+αB

• (α+β)A=αA+βA

• (αβ)A=α(β)A

где A и B - прямоугольные матрицы, α и β - числа из поля K.

Теперь рассмотрим такое понятие, как разность матриц. Формально эту операцию можно представить так:

По свое сути, разность матриц это поэлементное вычитание. Разумеется, как и в случае со сложением, размеры матриц должны совпадать. 

Пример 5. Вычислим разность матриц:

Решение:

Теперь рассмотрим умножение матриц. Путь у нас есть зависимость величин z₁, z₂, ..., z_m от y₁, y₂, ..., y_m через преобразование:

и зависимость величин y₁, y₂, ..., y_n от x₁, x₂, ..., x_n через преобразование:

Тогда мы можем применить составное преобразование, если подставим в формулу для z₁, z₂, ..., z_m значения из формулы (2.10):

В соответствии с этим имеет место следующее определение: произведение двух прямоугольных матриц

и

называется матрица

У которой каждый элемент c_ij, стоящий на пересечении i-ой строки и j-ого столбца, равен произведению i-ой строки первой матрицы A на j-ый столбец второй матрицы B. Под произведением двух рядов чисел друг на друга  подразумевается сумма попарных произведений чисел в этих рядах. Таким образом:

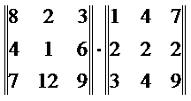
Операция произведения двух матриц называется умножением матриц.

Стоит заметить, что произведение матриц возможно только в том случае, когда количество столбцов в первом сомножителе равно количество строк во втором.

Пример 6. Найти произведение матриц:

Решение.

Пример 7. Найти произведение матриц:

Решение:

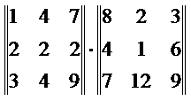
Стоит обратить внимание на тот факт, что для произведения матриц не действует закон перестановки множителей, даже если обе матрицы квадратные. Попробуем, например, найти произведение вот таких вот матриц (перестановка множителей из примера 7):

Результат будет совсем другой:

Но для некоторых частных случаев при перестановке матричных множителей произведение не меняется. Матрицы, входящие в такое произведение, называют перестановочными, или коммутирующими между собой. Пример:

и