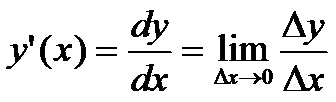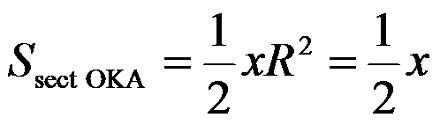| Математическое приложение для чайников. Урок 3. Дифференциал. Производная |

|

|
| Автор megabax | |||||
| 02.07.2020 г. | |||||
Математическое приложение для чайников. Урок 3. Дифференциал. ПроизводнаяЧто бы смотреть урок полностью, подпишитесь на платный раздел. В платном разделе статья находиться здесь. На уроке Математическое приложение для чайников. Урок 2. Интеграл функции x в степени n мы уже рассмотрели основы дифференцирования (доказывали формулу интеграла от xn через дифференцирование). Напомню лишь основные тезисы. И так, дифференциал - это скорость изменения функции. Например, если тело движется по какому то определенному принципу, и пройденный путь можно выразить математической формулой через время (t), тогда мы можем сказать что путь - это функция от времени - S(t). А скорость - это производная этой функции: v(t)=S'(t). Для того, что бы найти производную, необходимо бесконечно малое приращение(изменение) функции разделить на бесконечно малое приращение(изменение) аргумента. Такое отношение называется дифференциал и его можно выразить через предел (формула 2.2 из прошлого урока):
... ....Для чего мы делаем все эти построения? А для того, что бы доказать справедливость замечательного предела через ... ... ...Отсюда:
Определим площадь треугольника OAL... .... |
|||||
| Последнее обновление ( 02.07.2020 г. ) | |||||
| Пред. » |
|---|