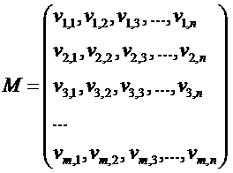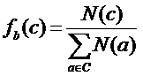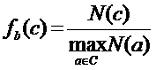| Математическое моделирование. Урок 2. От системы данных к системе с поведением. |

|

|
| Автор megabax | |||||||||
| 28.06.2020 г. | |||||||||
Математическое моделирование. Урок 2. От системы данных к системе с поведением.Для того, чтобы исследовать объект, ему сопоставляется какая то система. Как я уже говорил на прошлом уроке, под системой в рамках такого моделирования понимается совокупность элементов, организованных каким либо образом и взаимодействующих между собой. Как описать систему математически? Во-первых, каждому свойству объекта присвоим какую либо переменную. Во-вторых, введем такое понятие, как параметр. Следует четко различать разницу между пережду переменной и параметром. Так, переменной является образ свойства объекта, определяемый конкретной процедурой измерения. А параметр - это операционное представление, используемое для определения различий в наблюдениях одного и того же свойства. Для того, чтобы было более понятно, приведу примеры. Например, температура воздуха или скорость ветра в какой либо месте - это переменная. А вот время, в течении которого меняется температура - это параметр. Географическое положение места, где мы измеряем погодные условия - это тоже параметр. Система, задаваемая на объекте, называется системой объекта. Она представляет собой множество свойств и множество параметров. Для исследования объекта мы проводим наблюдение. Наблюдение - это упорядоченная пара параметр - совокупность зафиксированного полного значения переменных. Операция, вводящая конкретную переменную как образ свойств называют канал наблюдения. Обычно каналом является измерительный прибор и процедура, описывающая его применение. Множество таких пар называется функция данных. Переменные бывают входные и выходные. Входные переменные - это такие переменные, значения которых задаются извне. Факторы, влияющие на входные переменные, называются средой системы. Те переменные, которые определяются внутри самой системы, называются выходными. Если система имеет входные и выходные переменны, то это направленная система. Если такого разделения нет, то система нейтральная. Множество пар параметр - совокупность значения переменных образуют функцию d (функцию данных), отображающую полное параметрическое множество в полное множество состояний. Эта функция любому значению полного параметра ставит в соответствие одно полное состояние переменных. Говоря иными словами, функция d - это зависимость совокупности значений переменных от совокупности значения параметра. Можно сказать и так, что совокупность параметров - это аргументы функции d, а совокупность значений переменных - это результат данной функции. Другими словами, можно сказать, что совокупность значений параметров - это ключ, а совокупность значений переменных - это то, что найдено по этому ключу. Данные системы можно представить в виде такой вот матрицы: каждая строка матрицы соответствует совокупности значений параметров, а каждый элемент строки соответствует переменной, соответствующей данной совокупности параметров. Для анализа системы существует два подхода: вероятностный, когда мы имеем достаточно много данных и возможностный, когда количество данных ограничено. Основная характеристика системы - это функция поведения. Для вероятностного подхода эта функция вычисляется по формуле:
где N(c) - частоты состояний, aÎC - выборка для всех состояний. Для возможностного подхода функция поведения считается немножко по другому, там делим не на количество всех элементов выборки, а на максимальную частоту выборки:
Как правило, функция поведения считается для каждого варианта строки матрицы и все расчеты сводятся в таблицу. Далее я вам расскажу про эту таблицу. А сейчас один немаловажный момент. Дело в том, что значение переменных может быть задано самыми разнообразными вещественными числами. Чаще всего бывает так, что каждое число в выборе повторяется один единственный раз. Ну, может случайно два раза повторится. Ну, например, может быть так, что в выборке такие числа 0.1245345; 0.5345; 0.86234; 0.23556. Что мы делаем в этом случае? В этом случае мы выборку дискретизируем. Для этого мы каждой переменной, которая является вещественным числом ставим в соответствие некоторое целое число от 0 до L-1. Итак, пусть у нас есть некоторая система данных D=(I,d), заданная в виде таблицы:
где vj - вектор переменных системы,
заданный на параметрическом множестве
Эту таблицу вещественных чисел V мы преобразуем в дискретную таблицу (дискретизируем) по формуле:
где vi min - минимальное значение переменной в строке j, где vi max - максимальное значение переменной в столбце j, ɛ - некоторая малая величина порядка 10-10, она нужна для того, чтобы в результате ошибки округления не получилось так, что уровней дискретизации фактически не L, а L+1. На следующем уроке я это наглядно продемонстрирую. После преобразования по формуле (2.4) строится система с поведением, путем определения частот выборки по формулам (2.1) или (2.2). Построение подобных систем мы разберем в будущих уроках. Литература. 1. М.И. Пономорев, В. А. Тенев, Б. А. Якимович "Анализ данных с неопределенностью". Учебное пособие. Издательство ИжГТУ им. М. Т. Калашникова, Ижевск, 2014 288 стр.
|
|||||||||
| Последнее обновление ( 28.06.2020 г. ) | |||||||||
| « След. | Пред. » |
|---|