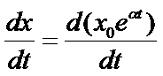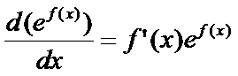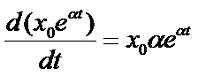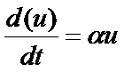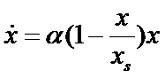Математическое моделирование. Урок 1. Введение.

Прежде чем изучать математическое моделирование, давайте определимся с терминологией. Сначала разберем сам термин моделирование. Итак, моделирование - это исследование какого либо объекта или системы объектов путем построения и изучения их моделей. Это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов. Соответственно, математическое моделирование - это построение и исследование именно математических моделей. Чтобы лучше это понять, давайте еще определимся с термином "модель".

В широком смысле модель  - это любой образ, аналог мысленный или установленный, а также изображение, описание, схема, чертеж, карта и т. п. какого либо объема, процесса или явления, используемый в качестве его заменителя или представителя. Если говорить научным языком, то модель - система, воспроизводящая для целей познания существенные характеристики исследуемого объекта. Сам объект, процесс или явление называется оригиналом данной модели. Соответственно, в рамках математического моделирование, так называемая математическая модель - это математическое описание объекта, по сути, набор формул, по которым мы можешь просчитать объект, в частности, прогнозировать его поведение. 

Может возникнуть вопрос: а для чего вообще нужно моделирование? Об этом я писал в отдельном уроке Моделирование систем. Урок 1. Введение. Там же я рассмотрел простейшую математическую модель: камень, брошенный под углом к горизонту. В рамках данного урока я познакомлю вас с другими, более сложным примерами применения математического моделирования.

Итак, вот несколько примеров, где можно применить математическое моделирование:

• Численное моделирование взрывоопасных ситуаций в сушильной камере. Краткая суть: окрашенная деталь помещается в сушильную камеру, где сушиться нагретым воздухом. Однажды эта камера взорвалась. Чтобы предотвратить возможность повторного взрыва, была построена математическая модель потоков воздуха, существующих в этой сушильной камере, которая позволила прогнозировать подобные взрывоопасные ситуации.

• Моделирование венчурного инвестирования.  Данная модель позволяет делать прогноз развития венчурного инвестиционного проекта (проекта с высоким риском), а именно, прогнозировать вероятностную картину распределения прибыли по будущим временным периодам и выбора оптимального момента для выхода инвестора из проекта.

• Математическая модель процесса обучения. Эта так называемая модель баланса знаний. Ее суть в том, что обучающегося человека представляют как некий объект, в которого втекают знания, часть этих знаний он усваивает, это повышает его уровень знаний. Со временем знания забываются и уровень знаний падает. При достижении определенного уровня знаний обучаемый человек сам начинает генерировать знания.

• Моделирование ценовой политики в условиях конкуренции. В данной модели используется интегральное исчисление и дифференциальные уравнения для решения двухкритериальной задачи оптимального управления.

• Нечеткая модель производства продукции. В такой модели структурная схема управления капиталом предприятия представлена в виде графа.

• Модель государственного управления экономикой. В модели представлена связь ВПП государства с различными факторами.

• Продолжение временных рядов. Временный ряд или последовательность преобразуется в матрицу с помощью сдвига по времени или лага определенной длины. На основании этой матрицы производиться обучение ИНС (искусственной нейронной сети). После этого нейросеть делает прогноз продолжение временного ряда.

• Задача скоринга. Строиться статистка возвратов и невозвратов кредитов по таким параметрам, как размер запрашиваемого кредита, срок кредита, доход клиента, рабочий стаж  и прочее. На основании этой статистики производится решение о выдаче кредита или отказе в выдаче кредита.

• Задачи интерпретации геофизических данных. Геофизические данные, которые используются для принятия решения о бурении скважин, обрабатываться при помощи искусственной нейронной сети.

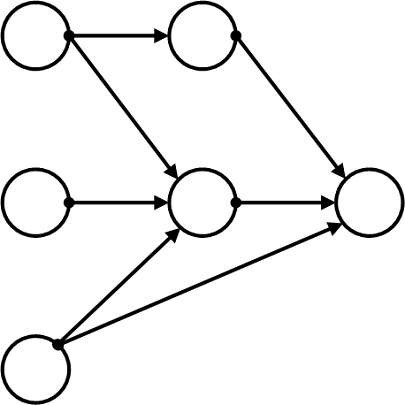
Одним из главных направлений математического моделирование является системное моделирование. Под системой в рамках такого моделирования понимается совокупность элементов, организованных каким либо образом и взаимодействующих между собой. Связь между элементами - это ограничение их степени свободы. Элемент - это предел разбиения системы с точки зрения решения конкретной задачи.

Графически систему можно представить в виде примерно такой схемы:

Здесь кружочками обозначены элементы системы, а стрелками - взаимодействия между элементами (связями). Математически связи можно описать следующими способами:

1. Алгебраические функции или выражения.

2. Дифференциальными уравнениями.

3. Логическими правилами и системами логического вывода.

Для примера рассмотрим относительно простую математическую модель, так называемую модель Мальтуса. Эта модель роста популяции какого либо вида живых существ. В этой модели скорость роста популяции описывается уравнением:

где α - некий параметр, определяющий разницу между рождением и смертностью. Решением этого уравнения является экспонентальная функция

Докажем это, подстановкой:

 Согласно формуле дифференцирования экспонентальной функции

Вычисляем (в нашем случае f(t)=αt):

Обозначим x₀αe^αt за u, тогда

Что и требовалось доказать.

Надо заметить, что при достижении какого то определенного объема данная модель перестает быть адекватной, так как не учитывает ограниченность ресурсов. Более адекватная модель выглядит так:

где x_s - равновесный размер популяции, при котором она не может дальше расти.

Литература.

1. М.И. Пономорев, В. А. Тенев, Б. А. Якимович "Анализ данных с неопределенностью". Учебное пособие. Издательство ИжГТУ им. М. Т. Калашникова, Ижевск, 2014 288 стр.

2. Википедия "Математическая модель". Статья в интернет, дата обращения 24.10.2015.