| Математический анализ для чайников. Урок 2. Множества. Решения задач. |

|

|
| Автор megabax | |
| 12.08.2014 г. | |
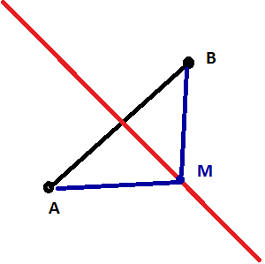
Математический анализ для чайников. Урок 2. Множества. Решения задач.На прошлом уроке мы с вами изучали множества. Сегодня от теории перейдем к практике. Будем решать задачи. Задача 1. Составить список элементов множества A={x : x Î N, -5≤x<4}, где N - множество натуральных чисел. Решение. Натуральные числа - это целые числа, они не могут быть меньше нуля. Поэтому, хотя у нас -5≤x, первое число из множества будет 1. Последнее 3, так как x<4. Таким образом A={1,2,3}. Задача 2. Описать множество M точек числовой прямой, таких, что {M:|OM|=2}, где O - точка начала координат. Решение. Данное множество задано характеристическим свойством - его элементы есть точки, равноудаленные от точки начала координат - O. Это две точки, -2 и 2. Таким образом, M = {-2,2} Задача 3. Верно ли соотношение {a, b, c}={{a,b},c}? Решение. Первое множество имеет три элемента, второе два (при чем один из них сам является множеством), так что они никак не могут быть равны. Так что данное равенство неверно. Точно такой же вывод можно сделать из того, что первое множество не содержит элемент {a,b}, который есть во втором множестве. Задача 4. Найти все подмножества множества {a,b,c}. Решение. Всякое множество содержит в себе пустое множество Æ и само себя. Данное же множество содержит еще следующие подмножества: {a, b}, {a, c}, {b, c}, {a}, {b}, {c} - то есть, все сочетания элементов из исходного множества. Таким образом, множество подмножеств множества {a, b, c} будет множество из 8 элементов: Æ , {a, b, c}, {a, b}, {a, c}, {b, c}, {a}, {b}, {c} В общем случае, множество всех подмножеств заданного множества есть множество из 2n элементов, где n - количество элементов в заданном множестве. Задача 5. Верно ли утверждение, что если AÎB и BÎC то AÎC для любых множеств A, B и C. Решение. Пусть у нас A=1. Рассмотрим так же пример произвольного множества B={1,2}. В этом случае у нас выполняется условие AÎB. И, рассмотрим множество C={{1,2},3}. В этом случае у нас выполняется условие BÎC. Но вот условие AÎC не выполняется, в множестве C нет A=1, так есть множество {1,2}, но отдельной единицы нету. Таким образом, утверждение, что если AÎB и BÎC то AÎC для любых множеств A, B и C является неверным. Задача 6. Составить список элементов множества, заданных характеристическими свойствами: 1) A={x: x2-8x+15=0}; 2) A={x: xÎN, -11<x≤-3} Решение. 1) В первом случае решением будет множество корней квадратного уравнения x2-8x+15=0. Решаем. Находим дискриминант D=82-4*15=64-60=4. Первый корень x1=(8+Ö4)/2=5. Второй корень x2=(8-Ö4)/2=3. Таким образом A={3,5} 2). Во втором случае x должен быть положительным целым числом от -11 до -3. Но таких чисел нет, так как в указанном промежутке лежат только отрицательны числа. Тоесть, решением является пустое множество A=Æ Задача 7. Доказать, что если A={x : x2-7x+6=0} и B={1,6} то A=B. Решение. Подставим значения множества B в формулу x2-7x+6=0. Для элемента 1: 12-7*1+6=1-7+6=0 - равенство выполняется. Для элемента 6: 62-7*6+6=36-42+6=0 - равенство так же выполняется. Уравнение x2-7x+6=0 является квадратным, оно может иметь не более двух корней, таким образом, во множестве A не может быть больше двух элементов. Данное уравнение имеет два корня 1 и 6, это мы только что проверили путем подстановки. Таким образом, при заданных условиях A=B Задача 8. Описать множество M плоскости, таких, что 1) {M:|OM|=R} 2) {M:|OM|≤R} 3) {M:|AM|=|BM|} Решение: 1) Данное множество является множеством точек на окружности, с центром в точке O и радиусом R. 2) Данное множество является множеством точек внутри круга (включая окружность) с центром в точке O и радиусом R. 3) Множество точек прямой, проходящей через середину отрезка AB и перпендикулярной ему: Задача 9. Какая разница между A Ì B и A Î B? Решение. Первая запись означает вхождение множества A в множество B (где A ≠ B), а вторая принадлежность элемента A множеству B. Множество может входить в другое множество но не являться его элементом, например, множество {1,2} входит в множество {1,2,3} но не является его элементом. А вот число 1 является элементом множества {1,2,3}. Одно множество может являться элементом другого множества, например, множество {1,2} является элементом множества {{1,2},3}, но множество {1,2} не принадлежит множеству {{1,2},3}, Так как во множестве {{1,2},3} нет элементом 1 и 2, в нем есть элемент {1,2}, но это не одно и тоже что 1 и 2 по отдельности. Задача 10. Доказать, что {{1,2},{2,3}} ≠ {1,2,3}. Решение. Первое множество содержит элементы {1,2} и {2,3}. Второе множество содержит элементы 1,2,3. Ни один из элементов 1,2,3 не является ни элементом {1,2}, ни элементом{2,3}. Хотя числа 1 и 2 входят в множество {1,2}, но сами по себе не являться множествами, поэтому 1 ≠ {1, 2} и 2 ≠ {1,2}. Тоже самое можно сказать и о числах 2 и 3 и множестве {2,3}. Задача 11. Верно ли, что: 1). {1,2} Î {{1,2,3}, {1,3}, 1, 2}. 2). {1,2} Í {{1,2,3}, {1,3}, 1, 2}. Решение. Первое утверждение не верно, поскольку в множестве {{1,2,3}, {1,3}, 1, 2} нет элемента {1,2}. Второе утверждение верно, поскольку в множестве {{1,2,3}, {1,3}, 1, 2} присутствуют все элементы множества {1,2}, а именно 1 и 2. |
|
| Последнее обновление ( 12.08.2014 г. ) |
| Пред. » |
|---|