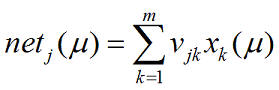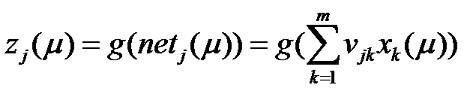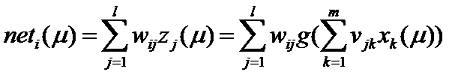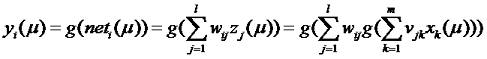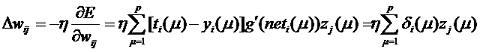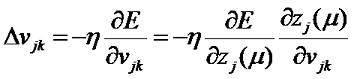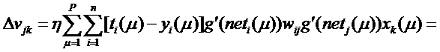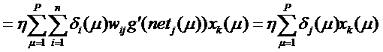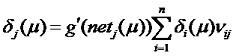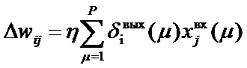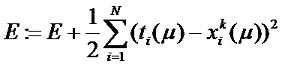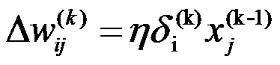| Теория нейронных сетей. Урок 6. Многослойный персептрон |

|

|
| Автор megabax | |||||||||||||||||||||||||||||
| 15.02.2014 г. | |||||||||||||||||||||||||||||
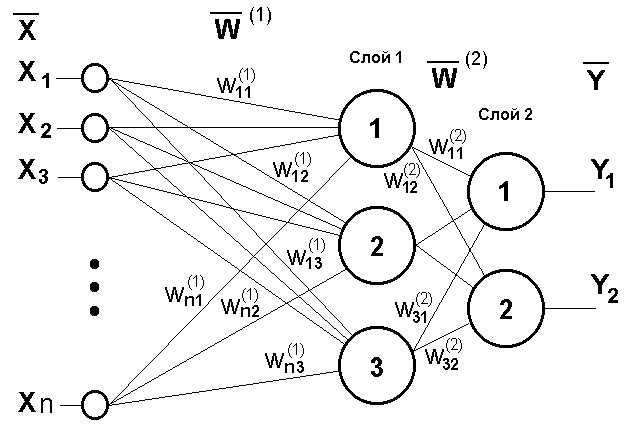
Теория нейронных сетей. Урок 6. Многослойный персептронЭто последний урок из серии "Теория нейронный сетей", публикуемый в бесплатном разделе. Начиная со следующего, публикация уроков будет продолжена в платном разделе. В бесплатном же разделе иногда, возможно, будут опубликованы некоторые отдельные статьи по нейронным сетям. Многослойный персептрон - это персептрон (см. урок 4), который состоит из нескольких слоев нейронов с прямым распространением сигналов. Обучение многослойного персептрона производиться на основе алгоритма обратного распространения ошибки. Данный алгоритм получается на основе обобщения дельта правила на многослойную нейросеть (о дельта правиле подробнее см. урок 5). И так, рассмотрим двухслойную нейронную сеть с прямыми связями: Определим реакцию i-ого выходного
слоя нейросети на входной вектор
И так, обозначим набор весов W(1) (см. рис.), как v, тогда сетевая функция j-ого скрытого слоя для μ-ого входного вектора вычисляется по формуле:
где j=1,2,3...,l Реакция j-ого нейронного слоя определяется из выражения:
Если набор весов W(2) обозначить как w, то сетевая функция i-ого нейрона выходного слоя вычисляется по формуле:
Исходя из этого, мы можем вычислить реакцию
i-ого нейрона выходного слоя на входящий вектор
Выведенные формулы соответствуют прямому распространению сигналов в рассматриваемой нейросети. Процесс обучения такого многослойного персептрона основан на минимизации ошибки, вычисленной методом градиента (см. предыдущий урок). Таким образом, изменение весов связей выходного слоя wij вычисляется по формуле:
где
Для изменения весов связей скрытого слоя vjk воспользуемся следующей схемой:
Отсюда:
где
Стоит обратить внимание на тот факт, что выражения (6.5) и (6.8) имеют одну и ту же форму. Отличие заключается в способе вычисления ошибок δi(μ) и δj(μ). Часто эти выражения записываются в виде:
Выражение (6.10) называется обобщенным дельта правилом. Согласно этому правилу, изменение веса связи между нейронами j и i пропорционально произведению ошибки δiвых(μ) на выходе нейрона i на его выходной сигнал, формируемый нейроном j. Предполагается, что слой, в котором находиться нейрон j, предшествует слою, в котором находиться нейрон i. Таким образом, для выходного слоя ошибка вычисляется по формуле (6.6) Для скрытых слоев ошибка вычисляется по формуле (6.9). То есть, ошибка каждого скрытого слоя вычисляется на основании ошибки предыдущего слоя. Это распространение ошибки в обратном направлении от входа к выходу. Алгоритм обратного распространения ошибки можно описать следующими шагами: 1. Выполнить инициализацию весов связей небольшими случайными значениями. Задать максимальную среднеквадратическую ошибку Emax. Текущее значение среднеквадратической ошибки НС приять 0 (E=0). 2. Подать на вход сети μ-ый входной вектор x(μ). 3. Выполнить распространение сигналов в соответствии с прямыми связями. 4. Вычислить среднеквадратическую ошибку:
и ошибку нейронов входного слоя:
5. Выполнить распространение ошибки в обратном направлении, руководствуясь правилом:
6. Обновить веса связей каждого слоя в соответствии с правилом:
7. Если μ<p тогда μ:=μ+1 и переходим к пункту 2, иначе переходим к пункту 8. 8. Проверить значение ошибки E. Если E<Emax, тогда закончить вычисления, в противном случае E:=0, μ:=1 и переходим к пункту 2. Рассмотренный алгоритм - это последовательный алгоритм. так как предполагает обновление весов при поступлении очередного входного вектора. Возможен другой вариант, когда, когда веса связей обновляются после поступления всех векторов обещающей выборки. Это будет уже блочный алгоритм.
|
|||||||||||||||||||||||||||||
| Последнее обновление ( 15.02.2014 г. ) | |||||||||||||||||||||||||||||
| Пред. » |
|---|