| Ориентация в пространстве. Урок 4. А-Алогоритм |

|

|
| Автор megabax | |||||
| 25.01.2014 г. | |||||
|
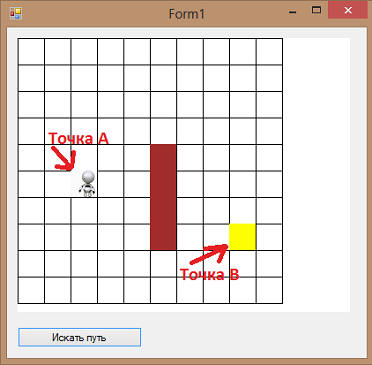
Ориентация в пространстве. Урок 4. А-Алогоритм Что бы смотреть урок полностью, подпишитесь на платный раздел. В платном разделе статья находиться здесь. На прошлом уроке мы разработали необходимые объекты, для того, что бы начать изучать алгоритмы ориентации в пространстве. Первый из алгоритмов, который мы изучим это алгоритм обхода препятствия: А-Алгоритм. Предположим, роботу надо попасть из точки А в точку B, и эти точки разделены стеной: При помощи А Алгоритма можно найти путь между этими двумя точками, который, в большинстве случаев, будет кратчайшим. Почему в большинстве? Дело в том, что это быстрый алгоритм. Он не перебирает все варианты (так как в некоторых случаях их может быть очень много, особенно на больших картах со сложной лабиринтообразной структурой). Кратко можно сформулировать этот алгоритм следующим образом: 1. Начинаем со стартовой точки A и
добавляем ее в "открытый список" клеток, которые нужно обработать. Открытый
список это что-то наподобие списка покупок. В данный момент есть только один
элемент в списке, но позже мы добавим еще. Список содержит клетки, которые может
быть находятся вдоль пути, который вы выберете, а может и нет. Проще говоря, это
список клеток, которые нужно проверить. Повторяем цикл до тех пор, пока не доберемся до исходной клетки или пока не обнаружим, что нам некуда идти. Как определить стоимость пути? Общем случае при движении по горизонтали и вертикали берем стоимость перемещения по клетке 1, а по диагонали 1.4 (путь по диагонали длиннее, данный коэффициент следует из теоремы Пифагора). Когда рассчитываем стоимость пути до пункта назначения, предполагаем, что мы движемся по горизонтали до того момента, пока координата x не станет равной координате точки назначения, затем по вертикали, пока не сравняется координата y. Ну, или наоборот, от перестановки слагаемых сумма не меняется. Расчет производиться следующим образом: сначала считаем стоимость перемещения в проверяемую соседнюю клетку, затем из нее в пункт назначения. Полученные результаты складываются. Стоимость не обязательно 1 и 1.4. В пространстве могут быть и такие объекты, которые препятствуют движению. Например, пространство может быть картой компьютерной игры, где есть болота, леса, горы. Описание этого алгоритма взяты из статьи Патрика Лестера (Patrick Lester) "Алгоритм A* для новичков.". Описано несколько сумбурно и не совсем понятно, но тем не менее, мы попробуем его реализовать, а потом будем понимать как он работает и оптимизировать. Но сначала создадим ряд вспомогательных классов...
... ...Для задач ориентации робота в пространстве (включая в том числе и А Алгоритм) мы создадим абстрактный класс Task:
Подробнее о методах. Тут есть один важный метод step - это шаг выполнения задачи. На каждом шаге робот будет выполнять определенные действия, до тех пор, пока задача не будет выполнена. В случае с A Алгоритмом мы сначала рассчитаем пусть, согласно этому алгоритму, а потом будем двигать робота по этому пути, вызывая метод step. В рамках данного урока реализуем алгоритм расчета:
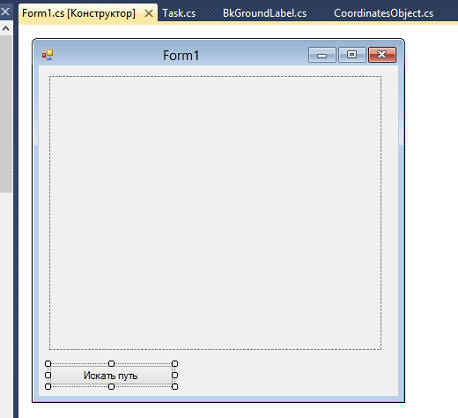
Добавим в форме кнопочку*: Слегка изменим модуль формы, в том числе и создадим обработчик нажатия на кнопочку:
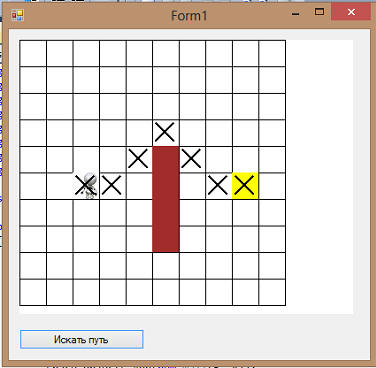
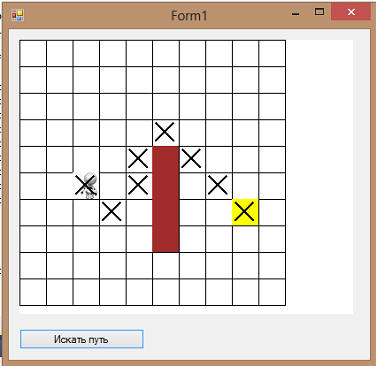
Тестируем: Как видим, алгоритм довольно корректно рассчитал путь. К сожалению, он делает это не всегда оптимально: Почему так происходит? Дело в том, ... .... ... Это не единственный подводный камень данного алгоритма. Но более подробно мы будем с ним работать на будущих уроках.
Скриншоты, помеченные знаком *, являются цитатами и иллюстрациями программного продукта "Microsoft Visual Studio 2010 Professional", авторское право на который принадлежит корпорации Microsoft.. |
|||||
| Последнее обновление ( 25.01.2014 г. ) | |||||
| Пред. » |
|---|