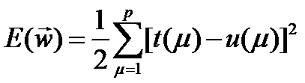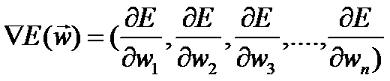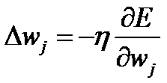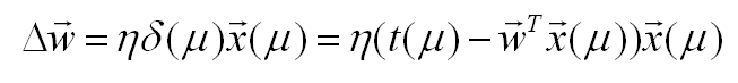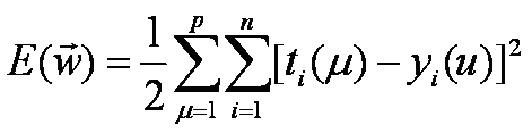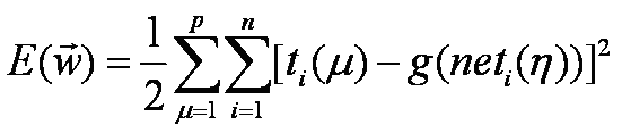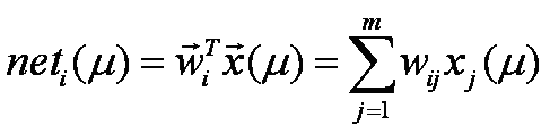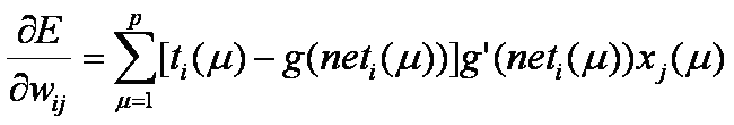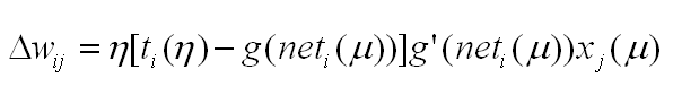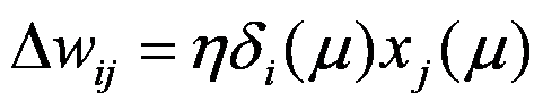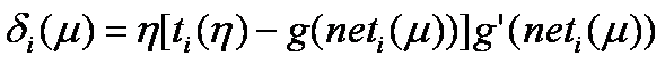Теория нейронных сетей. Урок 5. Адаптивный линейный элемент.

Адаптивный линейный элемент - это нейронный элемент с линейной функцией преобразования. По сути, это тот же персептрон (см. урок 4), но у него есть несколько отличий в принципе обучения. Суть в том, что вектор весовых коэффициентов корректируются так, что бы выходной сигнал u(μ) имел наилучшее приближение к желаемой функции t(μ). На практике минимизируется среднеквадратическое значение ошибки:

С целью минимизации ошибки применяется метод градиента: веса изменяются в направлении, обратном направлению градиента:

иными словами:

вычислим частную производную:

где

данное выражение называется ошибка адаптивного элемента.

Отметим, что в данном выражении суммирование  происходит по всем входным векторам . Поэтому веса изменяются после вычисления ошибок. На практике часто применяют последовательное обучение, при котором веса корректируются сразу после поступления на вход нейросети очередного входного вектора. Тогда:

Данное выражение называется правилом Уидроу-Хоффа. По своей структуре это по сути это правило обучения простого персептрона (см. урок 4). Казалось бы, вся разница только в способе вычисления ошибки. Данная формула получена в результате отказа от усреднения ошибки по всем входным векторам, что не гарантируем уменьшения среднеквадратической ошибки на каждом шаге. Кроме того, если правило обучение персептрона обеспечивает сходимость за конечное число шагов, то Уидроу-Хоффа, выведенное на основе метода градиента обеспечивает лишь асимптотическую сходимость при большем числе шагов.

Теперь обобщим правило Уидроу-Хоффа для однослойной нейросети с дифференцируемой функцией преобразования g(u). В этом случае среднеквадратическое значение ошибки вычисляется по формуле:

или:

где

значение сетевой функции i-ого нейрона при подаче на его вход входного вектора.

Применив к формуле вычисления среднеквадратической ошибки метод градиента, получим:

где производная функции преобразования нейросети.

Отсюда выводим дельта-правило обучения:

часто дельта правило записывают в виде:

где