Программирование - это просто - Генетический алгоритм. Урок 1. Решение многочлена

Генетический алгоритм. Урок 1. Решение многочлена

Автор megabax

07.07.2013 г.

unit AIObj

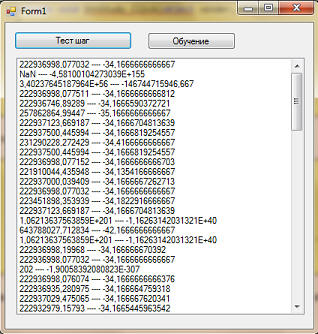
Генетический алгоритм. Урок 1. Решение многочлена

Что бы смотреть урок полностью, подпишитесь на платный раздел.

В платном разделе статья находиться здесь.

Исходники к уроку можно скачать в платном разделе.

Разговор двух блондинок:

- Ну что, поступила в Институт?

- Нет, не поступила.

- А что-ж так?

- Дык, задали мне решить какой то там квадратный трехчлен.

А я даже представить себе такого не могу!

Сегодня мы рассмотрим применение генетического алгоритма для решения многочлена степени три и более (поскольку уравнение степени два решаются легко любым адекватным школьником). Как можно решить, например, вот такое уравнение 5x⁵+7x⁴-8x³+4x²-11x-202? Ясно, что тупым перебором тут не отделаться, ибо нереально перебрать все числа. К тому же, у многочлена может быть не один корень. И тут на выручку нам приходит генетический алгоритм. Его муть состоит в том, оптимизируемые параметры кодируются в специальный формат, называемый генетическим кодом. Наборы таких параметров называются "особи", а совокупность "особей" - "популяцией". Для каждой "особи" вычисляется целевая функция, затем происходит сортировка и из "популяции" удаляются "особи" с наихудшим значением целевой функции. "Особи" могут "скрещиваться" между собой. Этот процесс происходит следующим образом: два "гена" рассекаются в случайном месте, и новый "ген" получается из соединения частей этих двух генов. Так же "особи" могут "мутировать". Суть мутации состоит в том, что случайным образом изменяется какой нибудь бит "гена".

Таким образом, путем естественно отбора, в выборе остаются только те комбинации параметров, которые лучшим образом соответствуют решению, например, имеют наименьшую целевую функцию. Если мы вычислим значение многочлена, и возьмем его по модулю, то это значение у нас должно стремиться к нулю....

....

....При нажатии на кнопочку "Тест шаг" у нас будет выполнятся переход к следующему поколению:

private void lbTest_Click(object sender, EventArgs e)

{

pop.NextGeneration();

show();

}

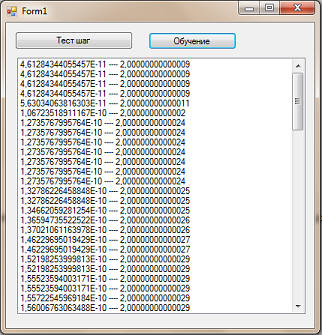
При нажатии на кнопочку "Обучение" у нас должно происходить генерация множества поколений, например, 100:

private void btnStudy_Click(object sender, EventArgs e)

{

for(int i=1; i<100; i++)

{

pop.NextGeneration();

}

show();

}

...

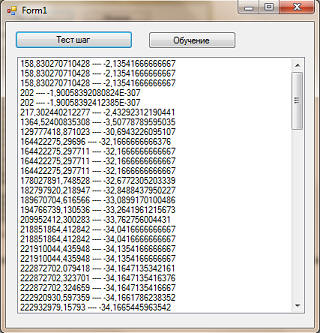
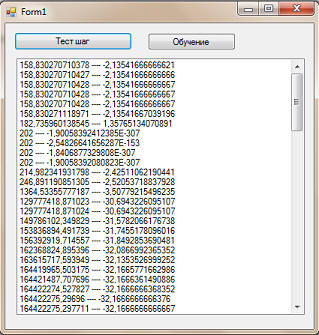
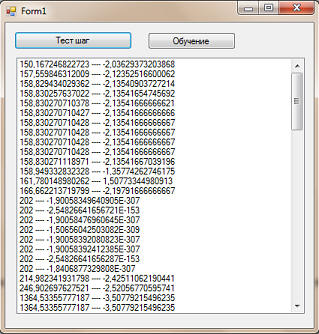
... Теперь перейдем к тестированию. И так, вот первоначальное поколение:

Как видим, и целевая функция даже близко не валяется с нулем. Жмем кнопочку "Тест шаг":

Жмем еще раз:

Как видим, количество видов лучшей целевой функцией увеличилась. В идеале, конечно, что бы она (целевая функция) достигла нуля. Жмем еще раз:

Что же мы видим? У нас появился вид с целевой функцией лучше, чем на прошлом шаге. В общем, с каждым шагам качество популяции улучшается. что будет, если мы пропустим 100 поколений? Вот, смотрите:

Фактически, у нас все особи имеют значение целевой функции, близкой к нулю (к идеальному значению). Тоесть, мы решили уравнение. Давайте проверим:

5x⁵+7x⁴-8x³+4x²-11x-202=5*2⁵+7*2⁴-8*2³+4*2²-11*2-202=5*32+7*16-8*8+4*4-22-202=160+112-64+16-22-202=0

Правда, все виды имеют только одно значение - 2. Но у многочлена, как вы знаете, могут быть несколько корней. но этим вопросом мы уже озадачимся на следующем уроке.

Скриншоты, помеченные знаком *, являются цитатами и иллюстрациями программного продукта "Microsoft Visual Studio 2010 Professional", авторское право на который принадлежит корпорации Microsoft..

Последнее обновление ( 07.07.2013 г. )

« След.

Вернуться