Создаем искусственный интеллект. Урок 2. Способы представления задач

Так как в системе искусственного интеллекта под решателем задач подразумевается компьютер, то способ представления задач должен быть удобным для их решения на ЭВМ. К таким способам можно отнести:

• Представления задач в пространстве состояний.
• Представление, сводящее задачи к подзадачам.
• Представление задач в виде теорем.

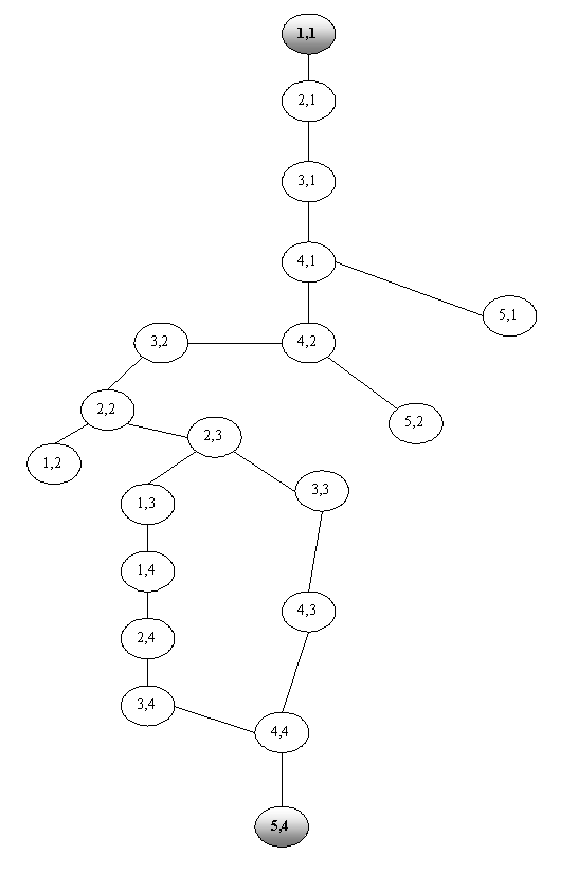
Теперь рассмотрим эти представления более подробно.

Представление задач в пространстве состояний.

Суть данного метода заключается в том, что бы в виде определенной структуры данных (чаще всего графа) задать начальные, конечные и промежуточные состояния, а так же операторы, преобразующие одно состояние в другое.

В качестве примера можно рассмотреть задачу нахождение пути в лабиринте, которая является основой для решения многих логистических задач (задача нахождения наиболее дешевого маршрута, наиболее выгодного расписания движения транспорта).

Предположим, нам необходимо из пункта A попасть в пункт B:

И так, начальное состояние задачи: точка (1,1). конечное состояние задачи точка (5,4). Кроме того, у нас имеется еще 18 промежуточных состояний - все остальные точки лабиринта. Оператор, меняющий состояния: "идти". Таким образом мы получаем граф возможных состояний:

Разумеется, нам необходимы еще правила применения операторов, преобразующих одно состояние в другое. Очевидно, что если данный граф мы будет просто обходить, то рискуем "зависнуть",  например, бесконечно блуждая по маршруту (2,3) -> (3,3) -> (4,3) -> (4,4) -> (3,4) -> (2,4) -> (1,4) -> (1,3) -> (2,3).

Сведение задач к подзадачам

Этот метод чем то напоминает способ представления задачи в пространстве состояний. Суть его заключается в том, что большая задача разбивается на несколько подзадач (декомпозиция), а те в свою очередь, так же разбиваются на подзадачи. И так до тех пор, пока мы не дойдем до самой маленькой задачи, которая может быть решена. Полученный таким образом граф (дерево решений) содержит вершину (начальное состояние), из которой исходят дуги к подзадачам, которые так же являются вершинами.

Вершины могут быть двух типов:

• Конъюнктивные (вершины типа И), когда для решения задачи требуется решить все входящие в нее подзадачи.

• Дизъюнктивные (вершины типа ИЛИ), когда для решения задачи достаточно решить хотя бы одну входящую в нее подзадачу задачу.

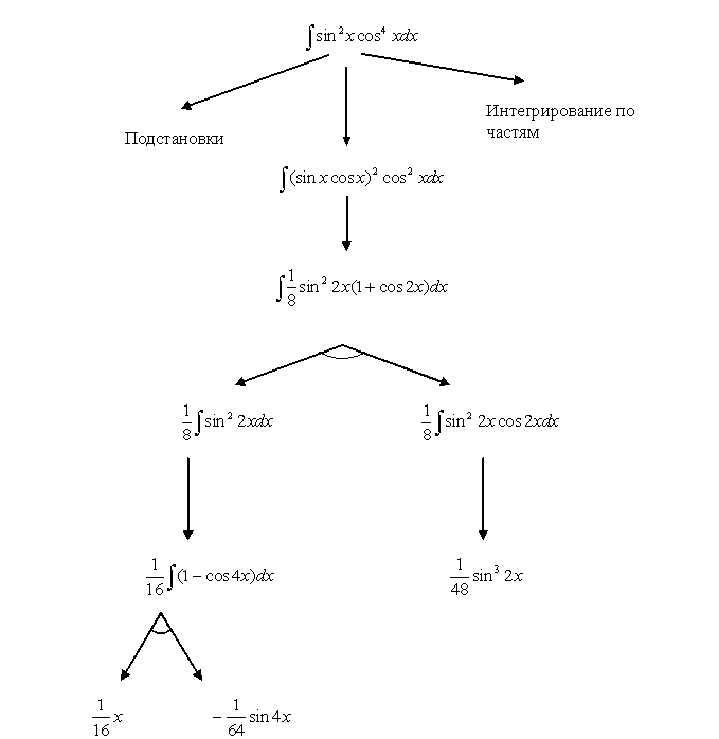
Давайте рассмотрим пример: нужно вычислить неопределенный интеграл . Дерево решений можно представить в таком виде (соединенные стрелки являются конъюнктивными вершинами:

Представление задач в виде теорем

Для представления задач в виде теорем используется специальный язык, описывающий логику предикатов (например, пролог). Процесс решения задачи протекает следующим образом:

Шаг 1. Формируется множество исходных истинных утверждений (аксиом).

Шаг 2. Строиться гипотеза относительно результатов решения задачи - целевое утверждение.

Шаг 3. Аксиомы комбинируются между собой на основании правил вывода.

Шаг 4. Проверяется, не содержит ли множество новых утверждений целевое утверждение или его отрицание. Если содержит, то процесс решения на этом заканчивается. Если нет - то полученное множество утверждений объединяется с исходными аксиомами и процесс повторяется.