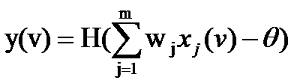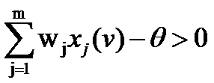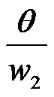Теория нейронных сетей. Урок 4. Обучение нейрости. Линейный персептрон.

Обучение нейросетей заключается в целенаправленном изменении весовых коэффициентов. Существует три вида обучения нейросетей:

Обучение с учителем.
Обучение без учителя.
Обучение с подкреплением.

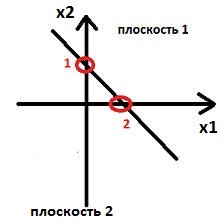
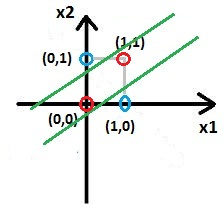
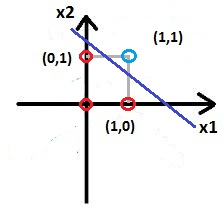
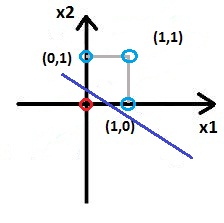
При обучении с учителем мы предполагаем, что для каждого v-ого входного вектора x(v), представляющего входной сигнал, мы заранее знаем выходной вектор ИНС t(v). Для корректировки весовых коэффициентов мы используем разность между желаемым выходным вектором t(v) и действительным выходным вектором y(v). Матрица весов модифицируется таким образом, что бы действительный выходной вектор приближался к желаемому. Множество примеров векторов разбиваются на две части - обучающая и тестовая. Цель обучения состоит в том, что бы нейросеть корректно отвечала на тестовые примеры, которые не входили в обучаемое множество векторов.

Но не всегда точно известна желаемая реакция ИНС. В некоторых случаях о желаемой реакции можно говорить с определенной долей вероятности. В этом случае управление весами нейросети производиться при помощи внешнего сигнала, который называется подкрепление.

Бывают случаи, когда желаемая реакция нейросети заранее неизвестна вообще. Тогда применяют обучение без учителя. В этом случае сеть должна быть самообучающейся, тоесть, самостоятельно обнаруживать какие либо закономерности. Такие ИНС еще называют самоорганизующимися сетями.

Теперь рассмотрим процесс обучения подробно. Начнем с обучения с учителем. Рассмотрим простой персептрон, реакция которого на входной вектор v определяется выражением:

где H() - единичная ступенчатая функция Хэвисайда (см. урок 1).

Задача обучения персептрона заключается в том, что бы найти вектор, который обеспечит совпадение желаемой t(v) и действительной y(v) реакции на входной вектор v. Ясно, что это будет в случае, если:

Данное выражение является линейным, и представляет собой уравнение гиперплоскости. Иными словами, задачи классификации векторов, решаемые при помощи простого персептрона, это линейно сепарабельные задачи.

Рассмотрим простой персептрон с двумя входами. Если представить, все его входные вектора на координатной плоскости, то работа персептрона будет заключаться в том, что бы определить, по какую сторону разделительной прямой лежит данный вектор:

Тогда координата точки 1 по оси x2 буте равна

а координата точки 2 по оси x1

Таким образом, линейный персептрон может классифицировать только такие образы, которые разделены при помощи гиперплоскости. На рисунке ниже изображена задача исключающего ИЛИ, которая не является линейно сепарабельной и не может быть решена с использование простого персептрона:

Красные точки на графике соответствуют ситуации, когда на выходе 0, голубые - когда 1, см таблицу истинности исключающего ИЛИ:

Вход 1	Вход 2	Выход
0	0	0
0	1	1
1	0	1
1	1	0

Таким образом, невозможно провести прямую так, что бы все красные точки был по одну сторону от прямой, а голубые - по другую.

А вот задачи И, а так же ИЛИ являются линейно сепарабельными, и их можно решать при помощи простого линейного персептрона. Давайте рассмотрим это на примере функции И. Вот ее таблица истинности:

Вход 1	Вход 2	Выход
0	0	0
0	1	0
1	0	0
1	1	1

И вот один из вариантов решения данной задачи:

Аналогично будет выглядеть решение и для ИЛИ:

См. таблицу истинности:

Вход 1	Вход 2	Выход
0	0	0
0	1	1
1	0	1
1	1	1

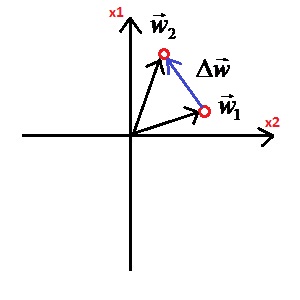
Обучается линейный персептрон следующим образом. На вход последовательно подаются вектора x(μ). Выходная реакция y(μ) сравнивается с желаемой реакцией t(μ). Если y(μ)=t(μ) - то ничего не делаем, персептрон уже обучен. В противном случае вектор w весов персептрона изменяется на величину Δw.

Величину корректировок весом находим по формуле:

Если порог θ рассматривать как дополнительный вес w₀, то разделяющая гиперплоскость будет проходить через начало координат, а изменение вектора w будет соответствовать вращению гиперплоскости вокруг точки начала rкоординат:

Последнее обновление ( 25.06.2013 г. )

« След.		Пред. »

Вернуться