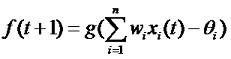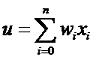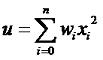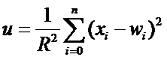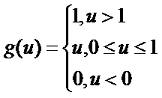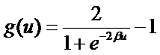Теория нейронных сетей. Урок 2. Сетевые функции и функции преобразование нейрона

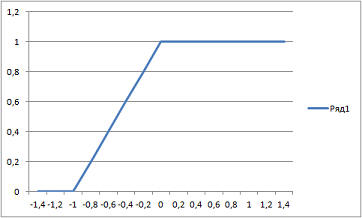
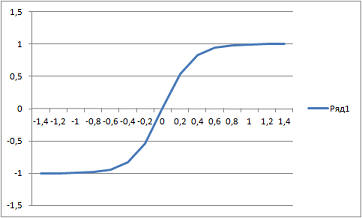
На прошлом уроке мы рассмотрели модель нейрона. В общем виде зависимость между входными и выходным сигналами выражается формулой:

где g - функция преобразования, u - сетевая функция. На прошлом уроке мы рассмотрели линейную сетевую функцию:

кроме нее широко используется так же квадратичная сетевая функция:

и радиальная (сферическая) функции:

Это самые распространенные виды сетевых функций. На сама деле их может быть гораздо больше. Я, например, в проекте "Генетический алгоритм" использовал вот такую:

См. шаг 6 проекта "Генетический алгоритм" а так же анонс урока "Пишем биржевого робота на C#. Урок 2. Нейросеть", "Пишем биржевого робота на C#. Урок 4. Доработка нейросети" и "Пишем биржевого робота на C#. Урок 5. Соединение нейросети с эмулятором биржевых торгов".

В качестве функции преобразование может быть использована ступенчатая функция (см. предыдущий урок):

линейная функция с насыщением:

Знаковая функция

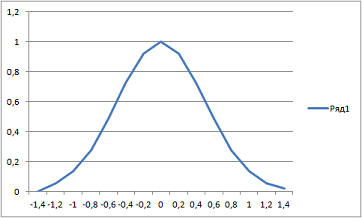
и, наконец, гауссова функция:

где c и σ - постоянные коэффициенты.

Если сетевая функция линейная, а функция преобразования ступенчатая или знаковая, то такие нейроны называются линейные, а нейросети на их основе нейронными сетями с линейными пороговыми элементами. Сигналы, распространяемые в таких сетях, являются бинарными и могут быть 0 или 1, либо +1 и -1. Если сетевая функция линейная, а функция преобразования сигмовидная (биполярная или униполярная), то такие нейросети называются нейронные сети с линейно-непрерывными элементами. Сигналы в них принимают произвольные значения от 0 до 1 или от -1 до 1.

Если пороговая функция равна 2, а весовые коэффициенты 1, то такой нейрон будет выполнять функцию "И" (для случая ступенчатой функции преобразования)

X1	0	1	1
X2	1	0	1
Y	0	0	1

А если у того же нейрона пороговое значение поставить 1, то это будет уже функция ИЛИ:

X1	0	1	1
X2	1	0	1
Y	1	1	1

Последнее обновление ( 05.03.2014 г. )

« След.		Пред. »

Вернуться