| Алгоритм сортировки методом Шелла. |

|

|
| Автор megabax | ||||||||||||||||||
| 31.12.2012 г. | ||||||||||||||||||
Алгоритм сортировки методом Шелла.Исходники к уроку можно скачать здесь. Данный алгоритм сортировки был изобретен Д. Л. Шеллом. Его суть состоит в том, что сначала мы сортируем, например, элементы отстоящие друг от друга на три позиции, потом на две и наконец, производим сортировку смежных элементов. Все эти сортировки делаем методом вставки. На самом деле могут быть другие шаги сортировки методом Шелла, главное, что бы последний шаг был равен 1. Источники утверждают*, наилучшая скорость достигается при последовательности 9,5,3,2,1. Вот сегодня мы и реализуем алгоритм сортировки Шелла именно с такой последовательностью. В рамках данного урока мы пока поверим источнику на слово, но в будущем обязательно потестим алгоритмы, что бы проверить, так ли это, а так же попробуем обосновать результаты наших тестов математически, в общем, займемся исследованиями. Но это в будущем, а сейчас просто закодим алгоритм:
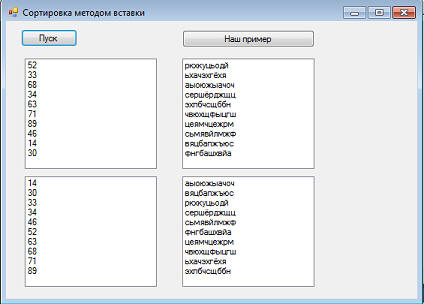
Приведенный метод мы вставляем в исходники прошлого урока, прямо в класс Sort<TType>. Лучше всего, сделать копию этих исходников, так как нам надо будет изменять еще и тестовый пример. Впрочем, изменять немного, просто все вызовы метода SortInsert заменим на SortShell, а внешний вид программы у нас не поменяется. Так что запускаем ее после наших изменений и тестим: Теперь посмотрим, как же алгоритм работает, для этого создадим какой либо тестовый пример, например 3,9,35,31,7,2,5,1,8,3. Навесим этот пример на кнопочку "Наш пример":
И через отладчик посмотрим, как идет процесс сортировки:
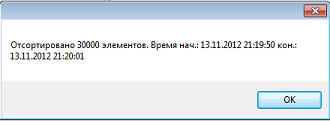
Так же на ютубте есть прикольный ролик, оригинально иллюстрирующий алгоритм сортировки методом Шелла http://www.youtube.com/watch?v=CmPA7zE8mx0. Теперь потестим и сравним алгоритм сортировки методом вставки и методом Шелла. Для начала алгоритм методом вставки:
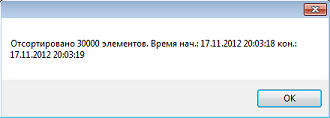
Смотрим результат (11 секунд). Теперь посмотрим метод Шелла:
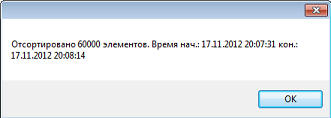
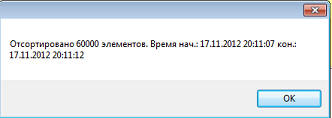
И вот результат работы этот программы: Как видим, время выполнения порядка 1 секунды, примерно в десять раз быстрее. Теперь попробуем увеличить количество сортируемых элементов до 60 тыс.:
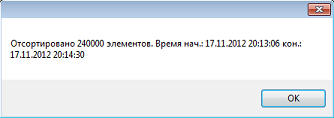
Смотрим время сортировки методом вставки: как видим, оно возросло до 43 секунды, примерно в четыре раза. А метод Шелла? Давайте и его проетстим: Почти пять секунд. А если увеличить размер массива до 240 тыс., в 4 раза? Давайте проверим: 84 секунды. Короче, примерно в 16 раз больше. Выходит, метод Шелла не такой уж хороший, хотя работает и быстрее алгоритма вставки. Как говорит источник*, количество сравнений при использовании алгоритма Шелла в степени 1.2 от числа элементов в сортируемом массиве. Но эксперимент показал, что это вовсе не так. Исходники к уроку можно скачать здесь. * Г. Шилдт, "Теория и практика С++". |
||||||||||||||||||
| Последнее обновление ( 31.12.2012 г. ) | ||||||||||||||||||
| « След. | Пред. » |
|---|