| Моделирование систем. Урок 4. Приблизим модель "Хищник, растение и травоядное" к реальности. |

|

|
| Автор megabax | |||||
| 03.12.2012 г. | |||||
Моделирование систем. Урок 4. Приблизим модель "Хищник, растение и травоядное" к реальности.Исходники к уроку можно скачать здесь. На прошлом уроке я обещал, что сегодня мы переделаем модель - пусть скорость роста растений задается в процентах. Для этого переделаем метод grow класса Plant:
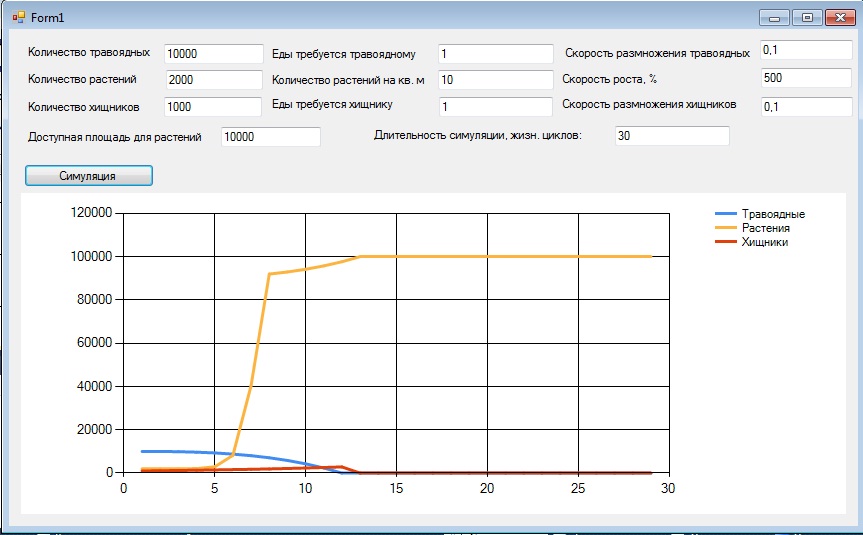
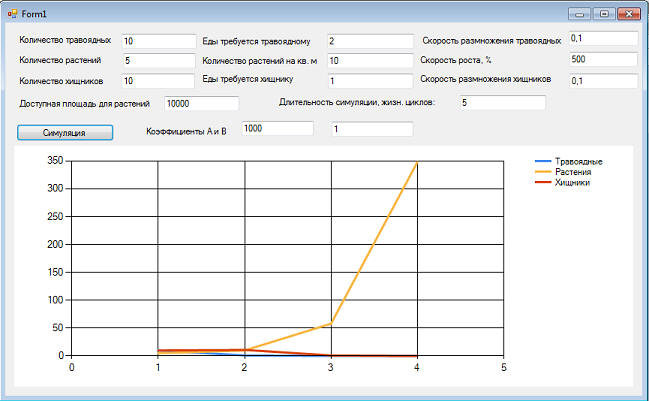
Теперь посмотрим, как все это отразилось на графике:
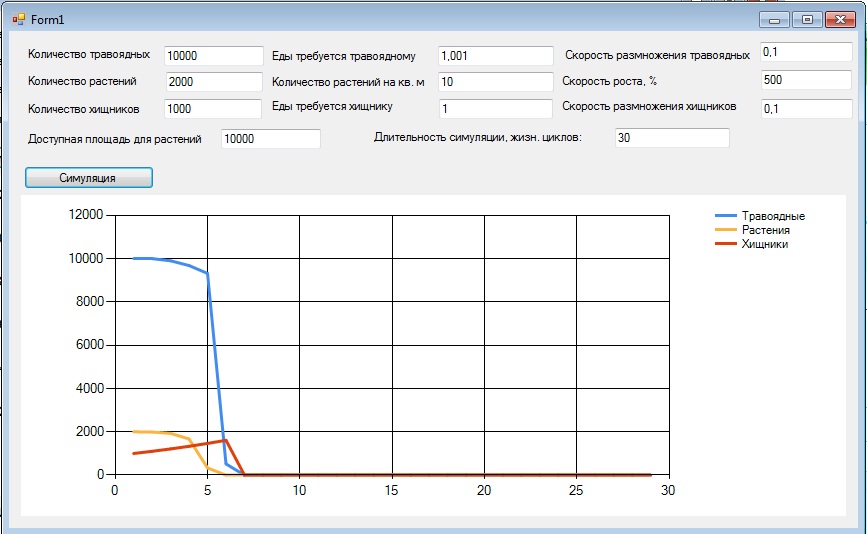
Как видим. все равно наблюдается коллапс, но сейчас может случиться и так, что растений не будет сосем:
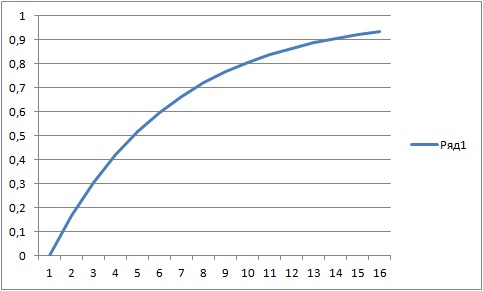
А теперь еще более приблизим модель к реальности. Предположим, что чем меньше травоядных, тем сложнее хищникам их поймать. Это мы можем реализовать, если при вычислении количества доступной еды будем размер популяции травоядных умножать на некую функцию f(x), где x- размер популяции. Чем меньше размер популяции, тем меньше коэффициент, но при бесконечной популяции он равен 1, при нулевой равен 0. Нам нужна функция наподобие такой:
на данном графике у нас изображена функция вида y=1-1/abx, где a и b - коэффициенты. И так, у класса Predator завидим пару свойств a и b:
Заводим новую функцию у этого же класса:
И переписываем метод liveLoop:
Теперь давайте посмотрим график развития ситуации:
Как видим, система все равно приходил к коллапсу. А теперь давайте подумаем, в каком случае система у нас будет в равновесии? Очевидно, что хищников должно быть такое число, что бы остановить рост травоядных и не дать им сожрать всю траву, иначе им нечего будет есть, травоядные вымрут, а вместе с ними и хищники. Предположим, что каждому хищнику нужно за один жизненный цикл одно травоядное. Скорость размножения как хищников, так и травоядных, 10%. Пусть у нас имеются и те и другие по 10 штук. Первый цикл. Хищников 11, травоядных 11. Но все 11 хищников съели всех травоядных Коллапс:
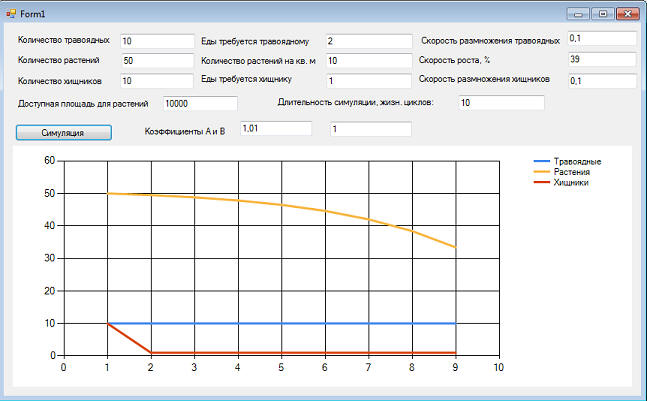
Но если при таком количестве травоядных хищникам трудно их будет поймать, и не все смогут "пообедать", то будет совсем другая картина:
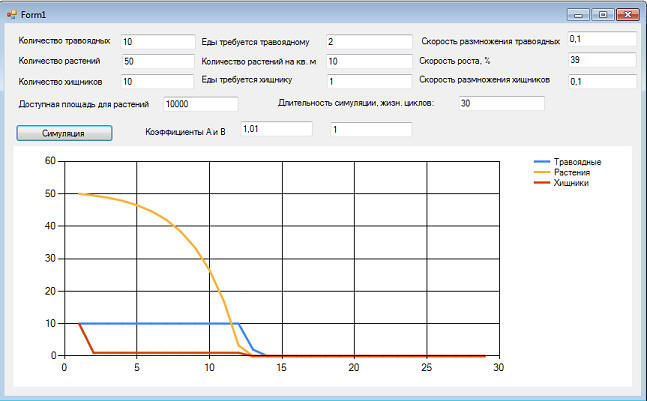
Но в этом случае система все равно движется к коллапсу:
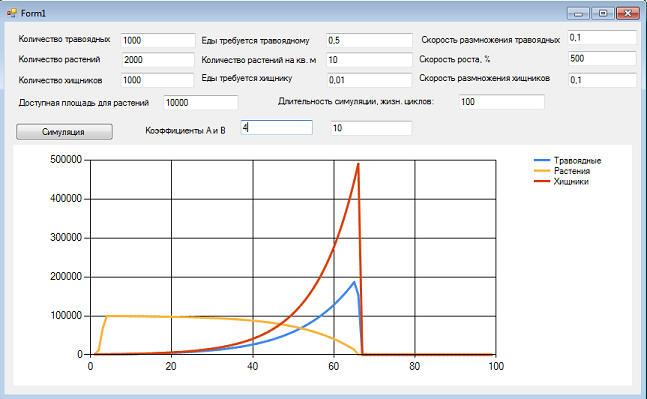
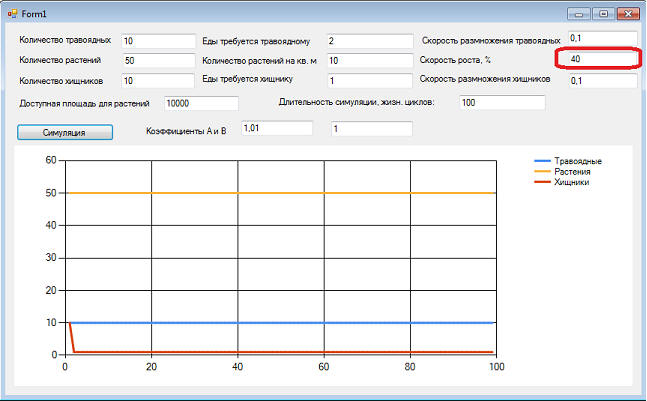
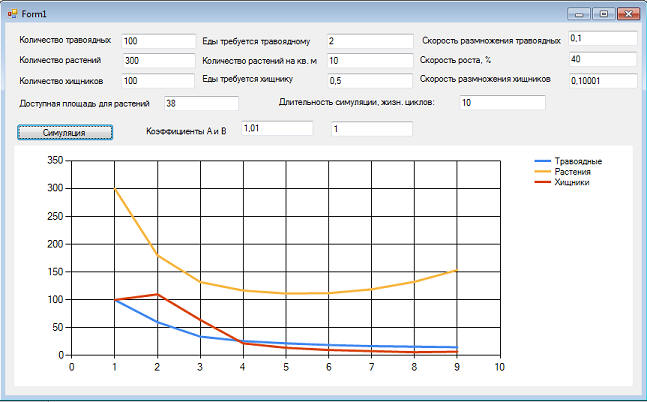
потому что количество траву катастрофически падает, и в один "прекрасный" момент травоядным нечего будет кушать. Они и вымрут. А вместе с ними и хищники. Спасет систему оптимальный прирост растений, если мы конечно, сможет его регулировать:
В данном случае для системы возможен приход к равновесию и при других исходных данных:
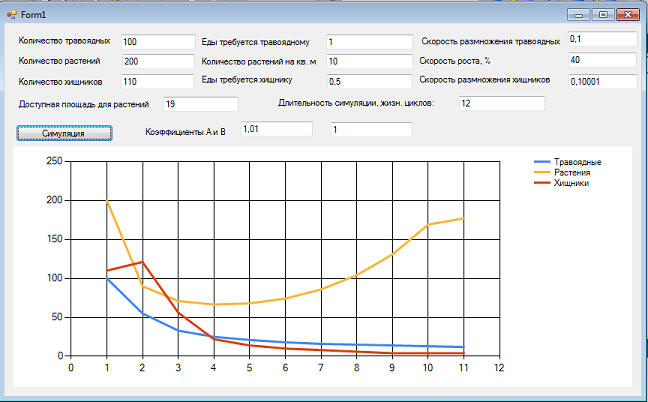
В том числе при разной начальной численности хищников и травоядных:
Скриншоты, приведенные в данной статье, являются цитатами и иллюстрациями программного продукта "Microsoft Visual Studio 2010", авторское право на который принадлежит Microsoft.
|
|||||
| Последнее обновление ( 03.12.2012 г. ) | |||||
| « След. | Пред. » |
|---|