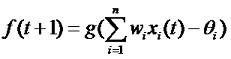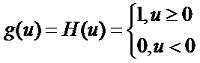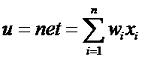| Теория нейронных сетей. Урок 1. Модель нейрона |

|

|
| Автор megabax | |
| 01.11.2012 г. | |
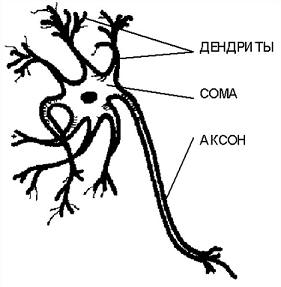
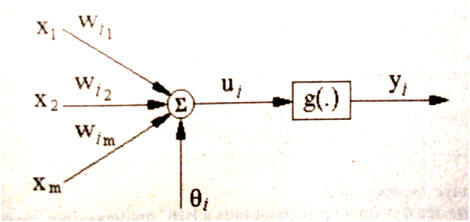
Теория нейронных сетей. Урок 1.Модель нейронаНейронные сети - это одно из перспективных направлений развития искусственного интеллекта. Здесь за основу взят принцип организации нервной системы живого существа. Теоретически, можно смоделировать даже мозг человека. Правда, практически это сделать в настоящее время не реально, так как мозг человека содержит 1011 нейронов. Каждый нейрон состоит из дендритов, сомы и аксонов:Дендриты - это ветвеобразные отростки, которые обеспечивают сбор информации от других нейронов или рецепторов. Тело нервной клетки называется сома. В ней происходят сложные биохимические процессы, благодаря которым происходят сложные нелинейные преобразования сигналов. Аксон - это отросток клетки, по которому выходной сигнал поступает на дендриты. Он разделяется на множество волокон. Место соединения аксонов с дендритом называется синапс. Сигналы, распространяющиеся в биологической нейронной сети, представляют собой короткие электрические импульсы. Под их воздействием изменяется потенциал самих нейронов. В момент достижения им некоторой пороговой величины вырабатывается импульс, который распространяется вдоль аксона. Потенциал сомы снижается, нейрон разряжается. Через некоторое время нейрон может снова сформировать импульс. Если импульсы, попадая на синапс повышают потенциал сомы, то это возбуждающий сигнал, если к понижению - тормозящий. При построении искусственной нейронной сети (ИНС), данную модель, как правило упрощают. В настоящее время существуют несколько моделей нейронов. И так, рассмотрим модель Маккаллоха и Питтса: которая выражается формулой: где g() - функция преобразования нейрона, θi - пороговое значение, n - количество входов нейрона. Для модели нейронной сети Маккаллоха - Питтса функцию g() можно выразить формулой: Эта функция так же называется функцией Хэвисайда H(u). Таким образом, если сумма входов, помноженных на коэффициенты, превышает θ, то на выходе нейрона мы получим 1, в противном случае 0. Стоит заметить, что выходной сигнал нейрона может меняться только в дискретные моменты времени. Функция, определяющая способ объединения входных признаков называется сетевой или базовой функцией. Она обозначается net. Сейчас мы разобрали лишь частный случай такой функции: На самом деле, сетевые функции и функции преобразования нейрона могут быть разные. Но об этом мы поговорим на следующем уроке. |
|
| Последнее обновление ( 01.11.2012 г. ) |
| « След. |
|---|