Учимся программировать в среде Metatrader (mql). Урок 25. Операторы управления циклом и множественного выбора.

Что бы смотреть урок полностью, подпишитесь на платный раздел.

В платном разделе статья находиться здесь.

Рассмотрим операторы управления циклами break и continue....

....

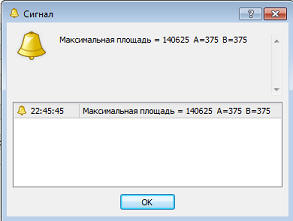
....Пусть перед нами стоит следующая задача: "Дана нить длиной 1,5 метра. Требуется сложить нить в форме прямоугольника, имеющего максимально возможную площадь. Путём последовательного перебора вариантов найти площадь этого прямоугольника и длины сторон с точностью до 1 см."

Из цельного отрезка нити можно сложить бесконечное количество прямоугольников различных размеров. Учитывая, что по условиям задачи точность вычислений составляет 1 мм, мы можем рассмотреть всего 749 вариантов. Первый, самый "тонкий", прямоугольник будет иметь размеры 1 х 749 мм, второй - 2 х 749 мм и так далее, а размеры последнего будут составлять 749 х 1 мм. Нам необходимо перебрать все эти прямоугольники и выбрать из них один, имеющий максимальную площадь.

Легко заметить, что в рассматриваемом наборе прямоугольников встречаются повторяющиеся размеры. Например, первый и последний прямоугольники имеют одинаковый размер: 1 х 749 (то же, что 749 х 1). Аналогично этому, размер второго прямоугольника совпадает с размером предпоследнего и т.д. Нам необходимо составить алгоритм перебора всех оригинальных вариантов, но перебирать повторяющиеся нет необходимости.
 

Решением данной задачи будет вот такой скрипт....

...

... И вот результат работы данного скрипта:

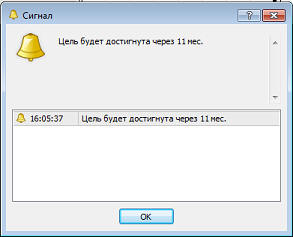
Теперь перейдем к continue. Так же рассмотрим его применение на примере решения задачи: "На первой ферме имеется 500 свиней. Ежедневно количество свиней  на первой ферме увеличивается на 2%. Если в конце месяца на первой ферме количество свиней превышает 40 000, то 7% свиней переводят на вторую ферму. Через какое время количество свиней на второй ферме достигнет численности 25 000? (Считать, что в месяце 30 рабочих дней.)".

Алгоритм решения задачи очевиден: необходимо организовать цикл, в котором рассчитывалась бы сумма общего количества свиней на первой ферме. По условию задачи перевод части свиней на вторую ферму происходит в конце месяца, значит необходимо создать ещё один (внутренний) цикл, в котором вычислялось бы накопление в текущем месяце. По окончании месяца необходимо выяснить: превышен ли пороговый уровень в 40 000? И если это так, то нужно рассчитать количество свиней, переводимых на вторую ферму в конце месяца, и общее количество свиней на второй ферме.

Решением данной задачи будет вот такой скрипт...

...

... И вот результат ее работы:

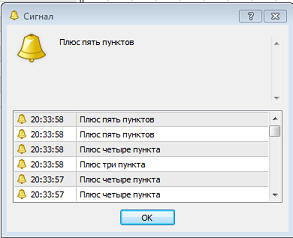
И у нас остался еще оператор ветвления...

...

... И вот результат работы данной программы:

...

Скриншоты, опубликованные в данной статье, являются цитатами и иллюстрациями  программного продукта "Metatrader 4", авторское право на который принадлежит "MetaQuotes Software Corp".