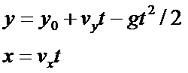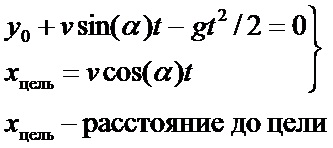| Моделирование систем. Урок 1. Введение. |

|

|
| Автор megabax | |
| 16.08.2012 г. | |
Моделирование систем. Урок 1. Введение.Прежде чем изучать моделирование систем, давайте ответим на вопрос, а для чего вообще нужно что то моделировать. Представим, нам нужно провести эксперимент, но его невозможно провести по одной из следующих причин:
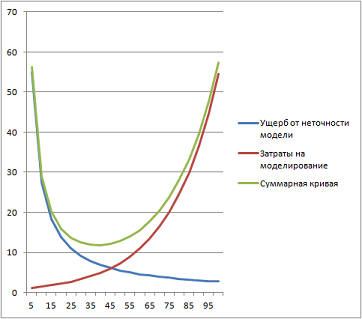
Процесс моделирования есть процесс перехода из реальной области в виртуальную (модельную) посредством формализации, далее происходит изучение модели (собственно моделирование) и, наконец, интерпретация результатов как обратный переход из виртуальной области в реальную. Этот путь заменяет прямое исследование объекта в реальной области, то есть лобовое или интуитивное решение задачи. Итак, в самом простом случае технология моделирования подразумевает 3 этапа: формализация, собственно моделирование, интерпретация. Если требуется уточнение, эти этапы повторяются вновь и вновь: формализация (проектирование), моделирование, интерпретация. Это так называемая спираль - вверх по кругу. Поскольку моделирование — способ замещения реального объекта его аналогом, то возникает вопрос: насколько аналог должен соответствовать исходному объекту? Существует два крайних варианта: Вариант 1: соответствие — 100%. Очевидно, что точность решения в этом случае максимальна, а ущерб от применения модели минимален. Но затраты на построение такой модели бесконечно велики, так как объект повторяется во всех своих деталях; фактически, создаётся точно такой же объект путём копирования его до атомов (что само по себе не имеет смысла). Вариант 2: соответствие — 0%. Модель совсем не похожа на реальный объект. Очевидно, что точность решения минимальна, а ущерб от применения модели максимален, бесконечен. Но затраты на построение такой модели нулевые. На самом деле модель создаётся из соображений компромисса между затратами на её построение и ущербом от неточности её применения. Это точка между двумя бесконечностями. То есть, моделируя, следует иметь в виду, что исследователь (моделировщик) должен стремиться к оптимуму суммарных затрат, включающих ущерб от применения и затраты на изготовление модели: Указанная на рисунке кривая является умозрительной и реально до начала моделирования построена быть не может. Поэтому на практике действуют таким образом: двигаются по шкале точности слева направо, то есть от простых моделей («Модель 1», «Модель 2»…) ко все более сложным («Модель 3», «Модель 4»…). А процесс моделирования имеет циклический спиралевидный характер: если построенная модель не удовлетворяет требованиям точности, то её детализируют, дорабатывают на следующем цикле. Улучшая модель, следят, чтобы эффект от усложнения модели превышал связанные с этим затраты. Как только исследователь замечает, что затраты на уточнение модели превышают эффект от точности при применении модели, следует остановиться, поскольку точка оптимума достигнута. Такой подход всегда гарантирует окупаемость вложений. В зависимости от носителя различают модели: натурные, мысленные, математические, имитационные, графические, фотографические и так далее. Каждая из моделей обладает различной способностью к прогнозу свойств объекта. Например, по фотографии человека в анфас вряд ли можно верно представить, как выглядит его затылок. Приближение в виде трёхмерной модели — намного лучше, но можно ли с её помощью определить, когда, например, у виртуального человека вырастут волосы длиной 50 см? Имитационная модель ещё более информативна. Но наибольшей ценностью обладают модели, пригодные для решения задач, то есть обладающие прогностическими свойствами, умеющие отвечать на вопросы. Следует различать два понятия — «модель» и «задача». Модель связывает переменные между собой законами. Эти законы действуют независимо от того, какая сейчас задача стоит перед нами. Модель объективна, она подобна миру, который нас окружает, и содержит в себе информацию об этом. Структура мира (в общем смысле) неизменна, фундаментальна, модель, следовательно, тоже. А человек, как существо субъективное, имеющее собственные цели, часто меняющиеся желания, ставит, в зависимости от своих потребностей, каждый раз новые задачи, требует решить возникающие у него проблемы. Он ставит вопросы к окружающему миру, с законами которого нельзя не считаться. Удобно ставить вопросы к модели, которая содержит нужную информацию о мире. Поэтому задача — это совокупность вопроса и модели. Можно к модели задавать все новые и новые вопросы и при этом не менять модель, но менять задачу. Рассмотрим простейший пример. Моделирование движения твердого тела, брошенного под углом к горизонту. Например, снаряд, выпущенный из пушки. Для чего можно использовать эту модель - например для того, что бы вычислить угол, под которым следует выпустить снаряд, что бы поразить цель. С точки зрения физики, данную модель можно представить в виде следующих математических формул (для двумерной системы координат):
Что бы вычислить угол наклона, нам нужно решить систему уравнений:
Разумеется, точность этой модели не идеальная, так как не учитывает ни неровность рельефа, ни скорость ветра, ни другие факторы (например, сопротивление воздуха). На этом вводный урок закончен, в следующих уроков будем писать на C# библиотеку для компьютерного моделирования различных процессов и систем, а так же будем писать примеры моделирования с использованием этой библиотеки. Скриншоты, приведенные в данной статье, являются цитатами и иллюстрациями программного продукта "Microsoft Visual Studio 2010", авторское право на который принадлежит Microsoft.
|
|
| Последнее обновление ( 16.08.2012 г. ) |
| « След. |
|---|