| Генетический алгоритм. Шаг 6. Как "зашить" в нейросеть торговые сигналы |

|

|
| Автор megabax | |
| 24.02.2011 г. | |
Генетический алгоритм. Шаг 6. Как "зашить" в нейросеть торговые сигналы
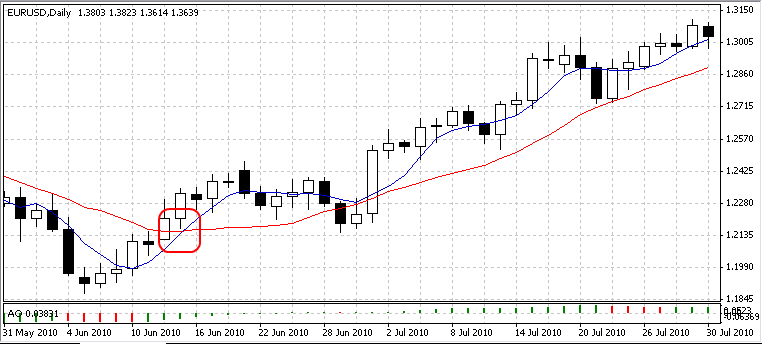
В прошлый раз я остановиться на том, что решил подумать, как закодировать торговые сигналы в нейронной сети. Рассмотрим, например, такой простой сигнал, как пересечение двух мувингов (быстрый и медленный)*:
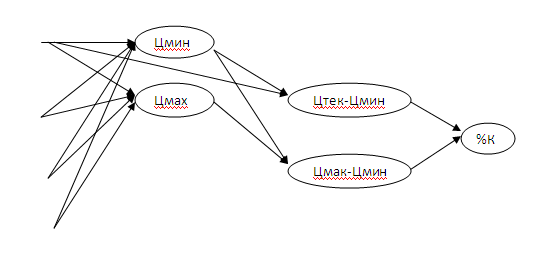
Простую MA можно представить в виде одного нейрона, у которого все весовые коэффициенты будут равны 1/кол-во входов. Для экспонентального свозящего среднего, соответственно, весовые коэффициенты для первых свечей будут больше, чем для последней. Так как у нас две скользящи средних, то на первый слой мы помещаем два нейрона. На втором слое у нас будет образовываться сигнал. Как в нейросети закодировать пересечение? Сразу рождается мысль поместить на первый слой еще два нейрона (уже 4), которые будут вычислять предыдущие значения индикаторов. И теперь нам надо как то связать воедино выходные сигналы этих четырех нейронов. А вот на втором слое мы поместим два нейрона, которые будут определять, тот факт, что один индикатор выше, другой ниже. Для этого у него будет всего два входа с коэффициента 1 и -1. Один нейрон обработает данные предыдущих значений индикаторов, другой текущий. Об передают данные на нейрон третьего слоя, тоже с коэффициентами 1 и -1. Но, немного проанализировав данную идею, я понял, что она не катит. И вот почему: пусть сначала первый индикатор был 100, второй 99. Первый нейрон вычислит 1. А текущее значение индикаторов, допустим, 101 и 103. Второй нейрон вычислит -2. В итоге будет -1. У нас нуль получиться только в том случае, когда оба индикатора на текущей и предыдущий свече отличаются друг от друга в одинаково разные стороны. В общем, не сможем мы на весовых коэффициентах выцепить пересечение. Но данную проблему решит особый вид нейрона - персептрон. В отличие от обычного нейрона, его выходной сигнал будет 0, если результат суммирования входов, умноженных на весовой коэффициент, будет ниже порога срабатывания, и 1 либо -1, если выше порога срабатывания в ту или иную сторону. Например, если порог срабатывания 0.1, то при 0,05 будет 0, при -0.03 будет 0, при 0.2 будет 1, при -0.11 будет -1. Таким образом, для реализации проверки пересечения нам понадобиться три персептрона: один для проверки текущих значений индикатора, второй для предыдущих, и третий для проверки результата этих двух персептронов, их логическое И. Логическое И у нас реализуется коэффициентами 1 и с порогом чувствительности 2. Если на входах будут обе единицы, то на выходе будет 2, которая преобразуется в 1. Если хоть на одном из входов 0 или -1, то результат на выходе будет меньше 2 и он преобразуется в 0. Теперь подумаем, как реализовать на нейросети более сложный индикатор, например, стохастик. Его линия %K вычисляется по формуле: %K=(Цтек-Цмин)/(Цмах-Цмин) где Цтек - текущая цена Цмин - минимальная цена за период стохастика, Цмах - максимальная цена за период стохастика вычитания у нас реализуется нейроном с весовыми коэффициентами 1 и -1. Тут проблем не возникнет. Как определить максимум и минимум? Думаю, на весовых коэффициентах это будет проблематично, поэтому считаю целесообразным завести еще несколько типов нейронов:
Таким образом, деление у нас будет реализовано именно геометрическим нейроном, где коэффициент второго входа будет -1, а первого 1. Иными словами, мы получим формулу: Вых=Вх1/Вх2=Вх11*Вх2-1 Вот так будет выглядеть структура нейросети для этой формулы: Похожим образом вычисляем и %D. Другие индикаторы я пока рассматривать не буду, думаю, возможностей перечисленных в данной статье типов нейронов будет достаточно. Если в дальнейшем выясниться, что нет, то всегда можно запрограммировать новые. Скриншоты, помеченные знаком*, являются цитатами и иллюстрациями программного продукта "Metatrader 4", авторское право на который принадлежит "MetaQuotes Software Corp".
|
|
| Последнее обновление ( 29.06.2011 г. ) |
| « След. | Пред. » |
|---|